创作声明：主要为李宏毅老师的听课笔记，附视频链接：https://www.bilibili.com/video/BV1Wv411h7kN?p=11

Critical Point

Critical Point的相关概念

在做Optimization的时候，你会发现，随着你的参数不断的update，你的training的loss不会再下降，但是你对这个loss仍然不满意，你可以把deep的network，跟linear的model，或比较浅的network比较，发现说它没有做得更好，所以 deepnetwork，没有发挥它完整的力量，有时候你会甚至发现，一开始你的model就train不起来，一开始你不管怎么update你的参数，你的loss降不下来，那这个时候到底发生了什么事情呢？

过去常见的一个估计，是因为我们现在走到了一个地方，这个地方参数对loss的微分为零，当你的参数对loss微分为零的时候，gradient descent就没有办法再update参数了，这个时候training就停下来了，loss当然就不会再下降了。

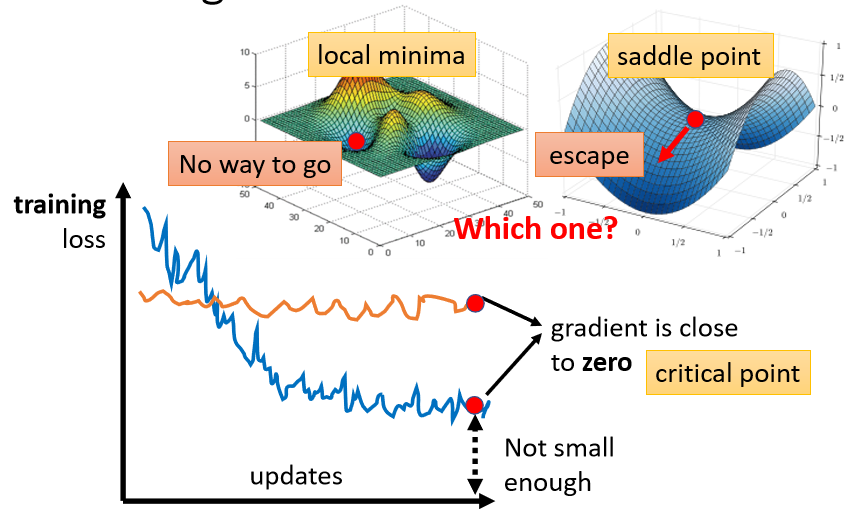
这个时候gradient为0，而且此时loss还是很高，没有发挥模型能力，显然不是global minima，那其实除了马上会想到的local minima，还有其他可能，比如说saddle point（鞍点），所谓saddle point，其实就是gradient是零，但不是local minima，也不是local maxima的地方，像在右边这个例子里面红色的这个点，它在左右这个方向是比较高的，前后这个方向是比较低的，它就像是一个马鞍的形状，所以叫做saddle point，中文就翻成鞍点。
gradient为零的点，统称为critical point（驻点），所以loss没有办法再下降，可以说是因为卡在了critical point，但不能说是卡在local minima，因为saddle point也是微分为零的点。

新的问题：gradient卡在了某个critical point，我们有没有办法知道，到底是local minima，还是saddle point？

回答这个问题很有必要，因为如果是卡在local minima，那可能就没有路可以走了，因为四周都比较高，你现在所在的位置已经是最低的点，loss最低的点了，往四周走loss都会比较高，你会不知道怎么走到其他的地方去，但如果你今天是卡在saddle point的话，saddle point旁边还是有路可以走的，还是有路可以让你的loss更低的。

区分local minima和saddle point

需要用到简单的数学知识，
判断说一个点到底是local minima，还是saddle point，需要知道我们loss function的形状，network本身很复杂，用复杂network算出来的loss function，显然也很复杂，虽然我们没有办法完整知道整个loss function的样子，但是如果给定某一组参数，比如说蓝色的这个在附近的loss function，是有办法被写出来的，它写出来如下：

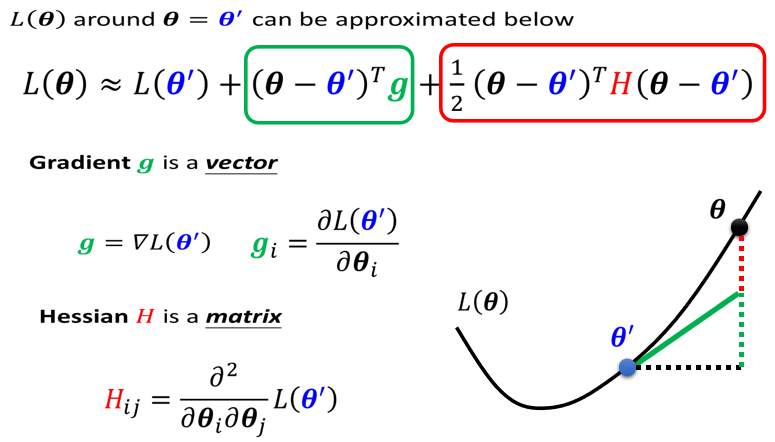
实际上是Tayler Series Approximation（泰勒级数展开）

g是一个向量，就是我们的gradient，我们用绿色的这个g来代表gradient，它的第i个component，就是θ的第i个component对L的微分。

H是一个矩阵，H里面放的是L的二次微分，它第i个row，第j个column的值，就是把θ的第i个component，对L作微分，再把θ的第j个component，对L作微分，再把θ的第i个component，对L作微分，做两次微分以后的结果就是这个$H_{ij}$

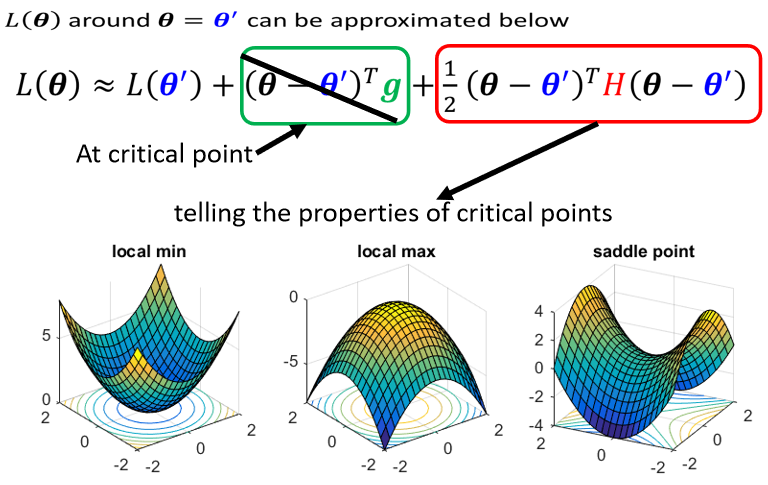
如果我们今天走到了一个critical point，意味着gradient为零，也就是绿色的这一项完全都不见了，只剩下红色的这一项，所以当在critical point的时候，这个loss function，它可以被近似为$L（\theta^{\prime}）$加上红色的这一项
我们可以根据红色的这一项来判断，在$\theta^{\prime}$附近的error surface，到底长什么样子，而知道Error surface长什么样子，我就可以判断$\theta^{\prime}$是一个local minima,是一个local maxima,还是一个saddle point。

方便起见，我们把$（\theta-\theta^{\prime}）$用$v$x向量来表示，判断方法如下：

逃离saddle point

只要$（\theta-\theta^{\prime}）$等于$u$，loss就会变小，所以你今天只要让$θ=u+\theta^{\prime}$，你就可以让loss变小只要沿着u，也就是eigen vector的方向，去更新你的参数去改变你的参数，你就可以让loss变小了。

所以虽然在critical point没有gradient，如果我们今天是在一个saddle point，你也不一定要惊慌，你只要找出负的eigen value，再找出它对应的eigen vector，用这个eigen vector去加$\theta^{\prime}$,就可以找到一个新的点，这个点的loss比原来还要低。

但是在实际的操作里，你几乎不会真的把Hessian算出来，这个要是二次微分，要计算这个矩阵的computation需要的运算量非常非常的大，更遑论还要把它的eigen value，跟eigen vector找出来，所以在实际的操作上，几乎没有人用这一个方法来逃离saddle point，之后的笔记会详细阐述其他有机会逃离saddle point的方法，他们的运算量都比要算这个H要小很多，这个方法是想说，如果是卡在saddle point，也许没有那么可怕，最糟的状况下你还有这一招，可以告诉你要往哪一个方向走。

从经验上看起来，其实local minima并没有那么常见，多数的时候往往是因为你卡在了一个saddle point。至于为什么，粗浅的解释是维度论，三维中封闭的东西，从四维轻松穿过，而向量的维度很多，那么是不是可以走的路就越多了呢，我们在训练一个network的时候，我们的参数往往动辄百万千万以上，所以我们的Error surface，其实是在一个非常高的维度中，我们参数有多少就代表我们的Error surface的维度有多少，参数是一千万就代表error surface，它的维度是一千万，既然维度这么高，会不会其实就有非常多的路可以走呢，那既然有非常多的路可以走，会不会其实local minima根本就很少呢，这是个尚待研究的问题。

Batch

之前说过实际上在算微分的时候，并不是真的对所有Data算出来的L作微分，而是把所有的Data分成一个一个的Batch

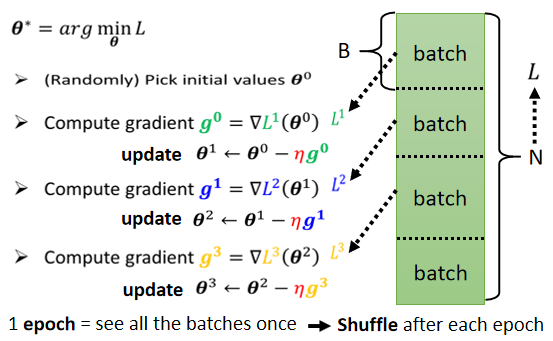
所有的Batch看过一遍，叫做一个Epoch，事实上，在做这些Batch的时候，你会做一件事情叫做Shuffle（洗牌），Shuffle有很多不同的做法，但一个常见的做法就是，在每一个Epoch开始之前，会分一次Batch，然后每一个Epoch的Batch都不一样。

回答之前的问题，为什么要用batch？

假设有20组数据，左边所有的数据都看过一遍才能够 Update 一次参数，右边所有资料看过一遍，你已经更新了20次的参数，但是左边这样子的方法有一个优点，就是它这一步走的是稳的，那右边这个方法它的缺点，就是它每一步走的是不稳的。
看起来左边的方法跟右边的方法，他们各自都有擅长跟不擅长的东西，左边是蓄力时间长，但是威力比较大，右边技能冷却时间短，但是它是比较不准的，看起来各自有各自的优缺点，但是你会觉得说，左边的方法技能冷却时间长，右边的方法技能冷却时间短，那只是你没有考虑并行运算的问题。

Larger batch size does not require longer time to compute gradient

事实上，比较大的Batch Size，你要算Loss，再进而算Gradient，所需要的时间，不一定比小的Batch Size要花的时间长。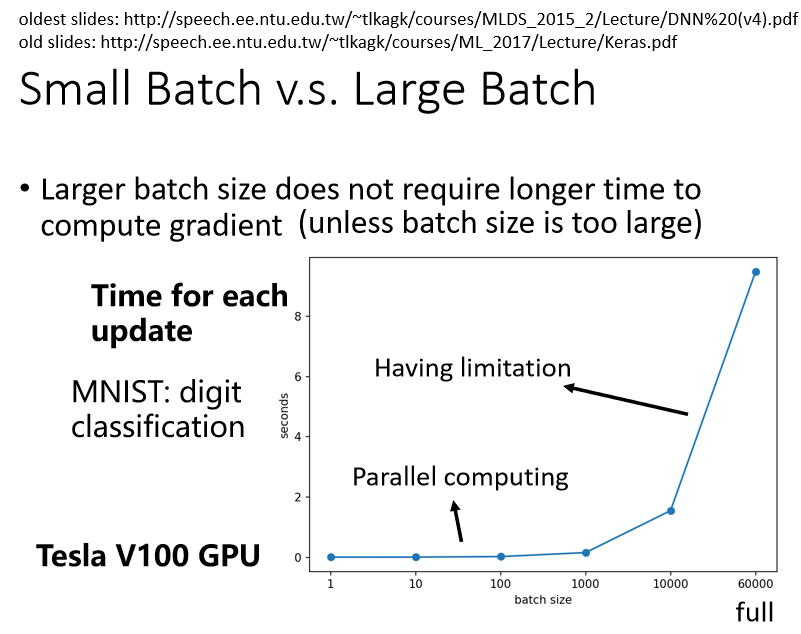

这边我们就是做了一个实验，我们想要知道说，给机器一个Batch，它要计算出Gradient，进而Update参数，到底需要花多少的时间。
这边列出了Batch Size等于1等于10，等于100等于1000所需要耗费的时间。
你会发现Batch Size从1到1000，需要耗费的时间几乎是一样的，你可能直觉上认为有1000组数据，那需要计算Loss，然后计算Gradient，花的时间不会是一组数据的1000倍吗，但是实际上并不是这样的
因为在实际上做运算的时候，我们有GPU，可以做并行运算，是因为你可以做并行计算的关系，这1000组数据是平行处理的，所以1000组数据所花的时间，并不是一组数据的1000倍，当然GPU并行计算的能力还是有它的极限，当你的Batch Size真的非常非常巨大的时候，GPU在跑完一个Batch，计算出Gradient所花费的时间，还是会随着Batch Size的增加，而逐渐增长。

所以如果Batch Size是从1到1000，所需要的时间几乎是一样的，但是当你的Batch Size增加到10000，乃至增加到60000的时候，你就会发现GPU要算完一个Batch，把这个Batch里面的资料都拿出来算Loss，再进而算Gradient，所要耗费的时间，确实有随着Batch Size的增加而逐渐增长，但你会发现这边用的是V100，所以它挺厉害的，给它60000组数据，一个Batch里面，塞了60000组数据，它在10秒钟之内也把Gradient就算出来了。

Smaller batch requires longer time for one epoch

GPU虽然有并行计算的能力，但它并行计算能力终究是有个极限，所以你Batch Size真的很大的时候，时间还是会增加的，但是因为有并行计算的能力，因此实际上，当你的Batch Size小的时候，你要跑完一个Epoch，花的时间是比大的Batch Size还要多的。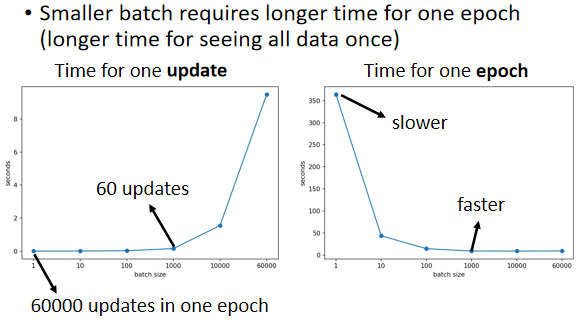

假设我们的训练数据只有6000组，那Batch Size设1，那你要60000个Update才能跑完一个Epoch，如果今天是Batch Size等于1000，你要60个Update才能跑完一个Epoch，而一个Batch Size等于1000和Batch Size等于1算Gradient的时间根本差不多，那60000次Update，跟60次Update比起来，它的时间的差距量就非常可观了。

在没有考虑并行计算的时候，你觉得大的Batch比较慢，但实际上，在有考虑并行计算的时候，一个Epoch大的Batch花的时间反而是比较少的。

那这样看起来大的Batch应该比较好？
大的BatchUpdate比较稳定，小的Batch，它的Gradient的方向比较Noisy，那这样看起来，大的Batch应该比较好，小的Batch应该比较差，因为现在大的Batch的劣势已经因为并行计算被拿掉了，它好像只剩下优势而已。

但神奇的地方是Noisy的Gradient，反而可以帮助Training，这个也是跟直觉正好相反的，大的Batch Size，往往在Training的时候，会给你带来比较差的结果，这个实际是Optimization的问题，当你用大的Batch Size的时候，你的Optimization可能会有问题，小的Batch Size，Optimization的结果反而是比较好的，为什么会这样子呢？

“Noisy” update is better for training

一个可能的解释是这样子的：

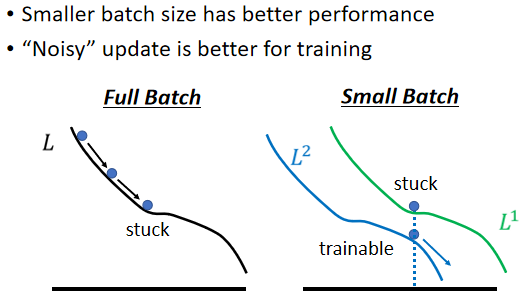
假设你是Full Batch，那你今天在Update你的参数的时候，你就是沿着一个Loss Function来Update参数，今天Update参数的时候走到一个Local Minima，走到一个Saddle Point，显然就停下来了，Gradient是零，如果你不特别去看Hession的话，那你用Gradient Descent的方法，你就没有办法再更新你的参数了，但是假如是Small Batch的话，因为我们每次是挑一个Batch出来，算它的Loss，Loss Function 定义不会变，但会因为数据的不同产生的 Error surface，你选到第一个Batch的时候，你是用L1来算你的Gradient，你选到第二个Batch的时候，你是用L2来算你的Gradient，假设你用L1算Gradient的时候，发现Gradient是零，卡住了，但L2跟L1又不一样，L2就不一定会卡住，所以L1卡住了没关系，换下一个Batch来，L2再算Gradient，所以今天这种Noisy的Update的方式，结果反而对Training，其实是有帮助的。

“Noisy” update is better for generalization

小的 Batch 也对 Testing 有帮助，这个实验结果是引用自On Large-Batch Training For Deep Learning，Generalization Gap And Sharp Minima，

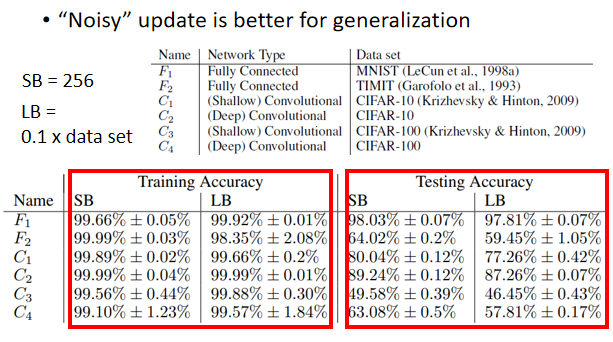
一个解释如图：

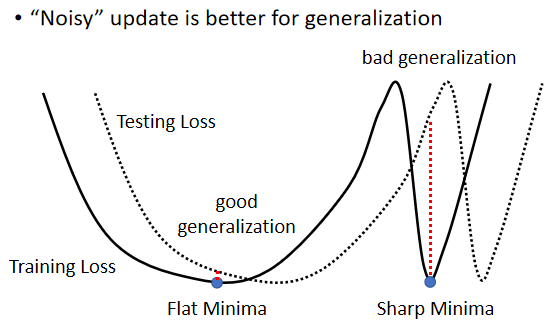
假设这个是我们的Training Loss，在这个Training Loss上面可能有很多个Local Minima，有不只一个Local Minima，那这些Local Minima它们的Loss都很低，它们Loss可能都趋近于0，但是这个Local Minima，还是有好Minima跟坏Minima之分。

如果一个Local Minima它在一个峡谷里面，它是坏的Minima，然后它在一个平原上，它是好的Minima，为什么会有这样的差异呢？

假设现在Training跟Testing中间，有一个Mismatch，Training的Loss跟Testing的Loss，它们那个Function不一样，有可能是本来你Training跟Testing的Distribution（分布） 就不一样。

那也有可能是因为Training跟Testing，你都是从Sample的Data算出来的，也许Training跟Testing，Sample到的Data不一样，那所以它们算出来的Loss，当然是有一点差距。

那我们就假设说这个Training跟Testing，它的差距就是把Training的Loss，这个Function往右平移一点，这时候你会发现，对左边这个在一个盆地里面的Minima来说，它的在Training跟Testing上面的结果，不会差太多，只差了一点点，但是对右边这个在峡谷里面的Minima来说，一差就可以天差地远。

它在这个Training Set上，算出来的Loss很低，但是因为Training跟Testing之间的不一样，所以Testing的时候，这个Error Surface一变，它算出来的Loss就变得很大，而很多人相信这个大的Batch Size，会让我们倾向于走到峡谷里面，而小的Batch Size，倾向于让我们走到盆地里面
他直觉上的想法是这样，就是小的Batch，它有很多的Loss，它每次Update的方向都不太一样，所以如果今天这个峡谷非常地窄，它可能一个不小心就跳出去了，因为每次Update的方向都不太一样，它的Update的方向也就随机性，所以一个很小的峡谷，没有办法困住小的Batch。

如果峡谷很小，它可能动一下就跳出去，之后停下来如果有一个非常宽的盆地，它才会停下来，那对于大的Batch Size，反正它就是顺着规定Update，然后它就很有可能，走到一个比较小的峡谷里面
但这只是一个解释，那也不是每个人都相信这个解释，那这个其实还是一个尚待研究的问题。

总结

在有平行运算的情况下，小的Batch跟大的Batch，其实运算的时间并没有太大的差距，除非你的大的Batch那个大是真的非常大，才会显示出差距来。但是一个Epoch需要的时间，小的Batch比较长，大的Batch反而是比较快的，所以从一个Epoch需要的时间来看，大的Batch其实是占到优势的。

而小的Batch，你会Update的方向比较Noisy，大的Batch Update的方向比较稳定，但是Noisy的Update的方向，反而在Optimization的时候会占到优势，而且在Testing的时候也会占到优势，所以大的Batch跟小的Batch，它们各自有它们擅长的地方。

所以Batch Size，变成另外一个你需要去调整的Hyperparameter。

那我们能不能够鱼与熊掌兼得呢，我们能不能够截取大的Batch的优点，跟小的Batch的优点，我们用大的Batch Size来做训练，用平行运算的能力来增加训练的效率，但是训练出来的结果同时又得到好的结果呢，又得到好的训练结果呢。

Momentum

Momentum（动量），这是另外一个，有可能可以对抗Saddle Point或Local Minima的技术，Momentum的运作如图：

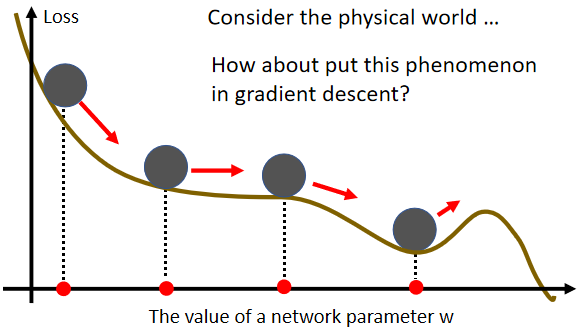
它的概念，可以想像成在物理的世界里面，假设Error Surface就是真正的斜坡，而我们的参数是一个球，你把球从斜坡上滚下来，如果今天是Gradient Descent，它走到Local Minima就停住了，走到Saddle Point就停住了,但是在物理的世界里，一个球如果从高处滚下来，从高处滚下来就算滚到Saddle Point，如果有惯性，它从左边滚下来，因为惯性的关系它还是会继续往右走，甚至它走到一个Local Minima，如果今天它的动量够大的话，它还是会继续往右走，甚至翻过这个小坡然后继续往右走
那所以今天在物理的世界里面，一个球从高处滚下来的时候，它并不会被Saddle Point，或Local Minima卡住，不一定会被Saddle Point，或Local Minima卡住，我们有没有办法运用这样子的概念，到Gradient Descent里面呢，这个就是Momentum技术。

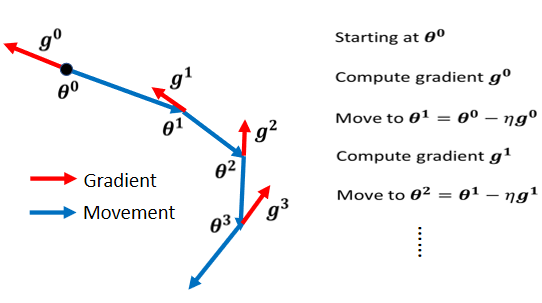
Vanilla Gradient Descent

Vanilla Gradient Descent（一般梯度下降） 如图：

Gradient Descent + Momentum

加上Momentum以后，每一次我们在移动我们的参数的时候，我们不是只往Gradient Descent，我们不是只往Gradient的反方向来移动参数，而是Gradient的反方向，加上前一步移动的方向，两者加起来的结果，去调整参数，如图：

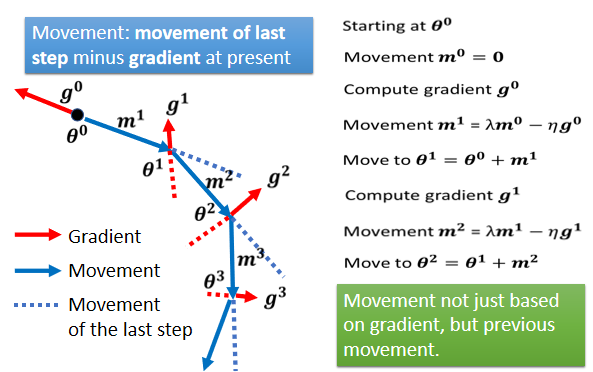
所谓的Momentum，当加上Momentum的时候，我们Update的方向，不是只考虑现在的Gradient，而是考虑过去所有Gradient的总和。

Adaptive Learning Rate

问题

critical point其实不一定是在训练一个Network的时候会遇到的最大的障碍，此话怎讲？

我们在训练一个network的时候，会把它的loss记录下来，所以会看到loss原来很大，随着你参数不断的update，横轴代表参数update的次数，随着你参数不断的update，这个loss会越来越小，最后就卡住了，你的loss不再下降。
多数这个时候，就会猜测是不是走到了critical point，因为gradient等于零的关系，所以我们没有办法再更新参数。当我们说走到critical point的时候，意味着gradient非常的小，但是你有确认过，当你的loss不再下降的时候，gradient真的很小吗？其实很多人可能并没有确认过这件事，而事实上在下面这个例子里面，当我们的loss不再下降的时候，gradient并没有真的变得很小。

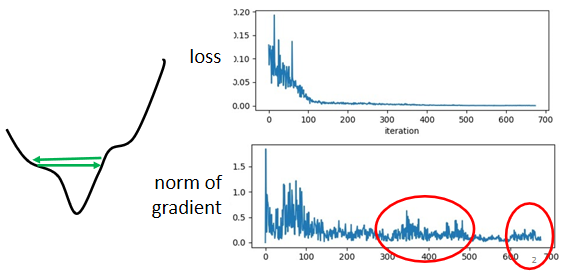
gradient是一个向量，下面是gradient的norm，即gradient这个向量的长度，随着参数更新的时候的变化，你会发现虽然loss不再下降，但是这个gradient的norm，gradient的大小并没有真的变得很小
这样的结果其实也不难估计，也许你遇到的是这样子的状况：

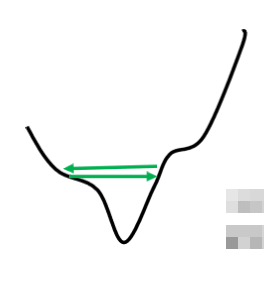
这个是我们的error surface，然后你现在的gradient，在error surface山谷的两个谷壁间，不断的来回的震荡,这个时候你的loss不会再下降，所以你会觉得它真的卡到了critical point，卡到了saddle point，卡到了local minima吗？不是的，它的gradient仍然很大，只是loss不再减小了。

举一个非常简单的例子，这边有一个非常简单的error surface：

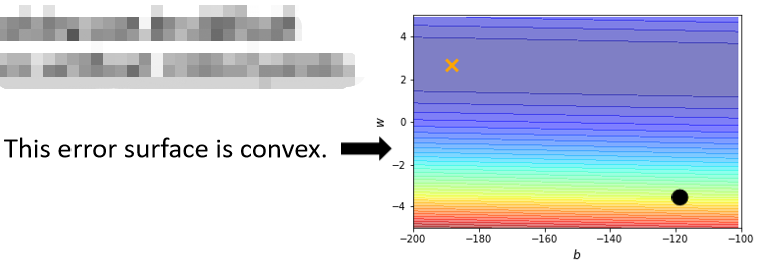
我们只有两个参数，这两个参数值不一样的时候，Loss的值不一样，我们就画出了一个error surface，这个error surface的最低点在黄色X这个地方，事实上，这个error surface是convex（凸面的） 的形状，convex optimization（凸优化）。

它的这个等高线是椭圆形的，只是它在横轴的地方，它的gradient非常的小，它的坡度的变化非常的小，非常的平滑，所以这个椭圆的长轴非常的长，短轴相对之下比较短，在纵轴的地方gradient的变化很大，error surface的坡度非常的陡峭，我们把黑点当作初始的点，然后来做gradient descend
你可能觉得这个convex的error surface，做gradient descend，有什么难的吗？不就是一路滑下来，然后再走过去吗，应该是非常容易。你实际上自己试一下，你会发现说，就连这种convex的error surface，形状这么简单的error surface，你用gradient descend，都不见得能把它做好，举例来说这个是实际的结果：

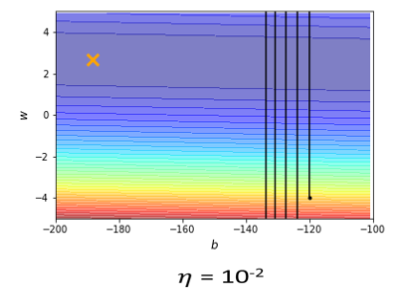
learning rate设10⁻²的时候，参数在山壁的两端不断的震荡，loss掉不下去，但是gradient其实仍然是很大的。

可能是因为你learning rate设太大了，learning rate决定了我们update参数的时候步伐有多大，learning rate显然步伐太大，你没有办法慢慢地滑到山谷里面，是不是只要把learning rate设小一点，就可以解决这个问题了。

事实不然，试着调整这个learning rate就会发现，仅仅要train这种convex的optimization的问题，就会很麻烦，调这个learning rate，从10⁻²一直调到10⁻⁷，调到10⁻⁷以后，终于不再震荡了。

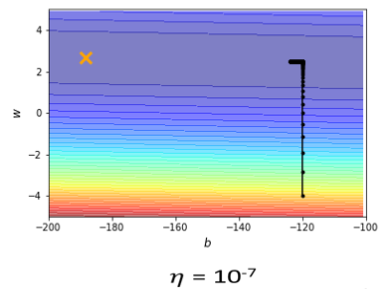
终于从这个地方滑到山低谷终于左转，但是会发现这个训练永远走不到终点，因为learning rate已经太小了，竖直往上这一段这个很斜的地方，因为这个坡度很陡，gradient的值很大，所以还能够前进一点，左拐以后这个地方坡度已经非常的平滑了，这么小的learning rate，根本没有办法再让我们的训练前进。

我们需要更好的gradient descend的版本，在之前我们的gradient descend里面，所有的参数都是设同样的learning rate，这显然是不够的，learning rate它应该要为每一个参数客制化。

客制化

其实我们可以看到一个大原则，如果在某一个方向上，gradient的值很小，非常的平坦，那我们会希望learning rate调大一点，如果在某一个方向上，gradient的值很小，非常的陡峭，那我们其实期待learning rate可以设得小一点。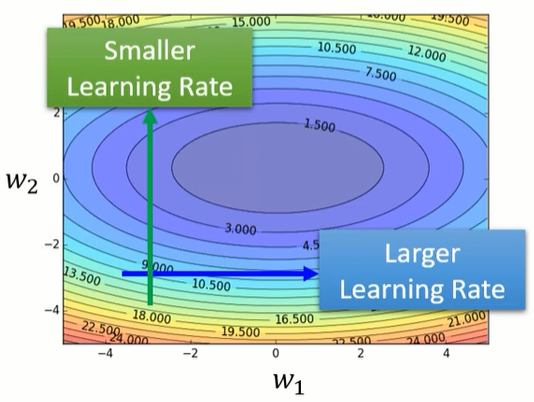

我们要改一下gradient descend原来的式子，我们只放某一个参数update的式子，我们之前在讲gradient descend，我们往往是讲所有参数update的式子，为了简化这个问题，我们只看一个参数，但是你完全可以把这个方法，推广到所有参数的状况。

$\theta_i^{t}$，在第t次迭代时第i个参数。

$g_i^{t}$代表θ等于θᵗ的时候，参数θᵢ对loss的微分，我们把这个θᵢᵗ减掉learning rate乘gᵢᵗ会得到θᵢᵗ⁺¹,这是我们原来的gradient descend，我们的learning rate是固定的。
现在我们要有一个随着参数客制化的learning rate，我们把原来learning rate这一项呢，改写成
$\frac{\eta}{\sigma_i^{t}}$，$\sigma_i^{t}$有一个上标t，有一个下标i，这代表说这个σ这个参数，首先它是depend on i的，不同的参数我们要给它不同的σ,同时它也是iteration dependent的，不同的iteration我们也会有不同的σ，此时我们就有一个parameter dependent的learning rate。
最后公式如下：

$\theta_i^{t+1}\gets \theta_i^{t}-\frac{\eta}{\sigma_i^{t}}g_i^{t}$

Adagrad

计算σ一个常见的类型是算gradient的Root Mean Square

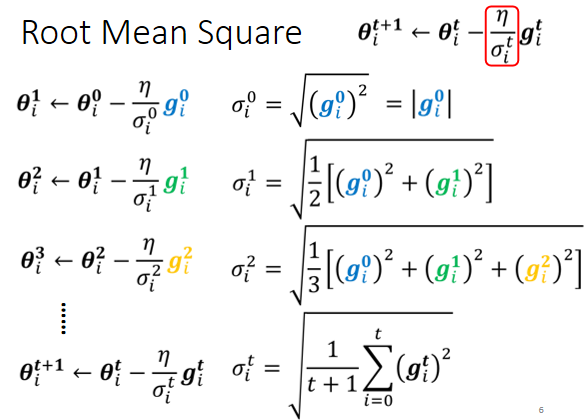
这一招被用在一个叫做Adagrad的方法里面，为什么它可以做到我们刚才讲的，坡度比较大的时候，learning rate就减小，坡度比较小的时候，learning rate就放大呢？

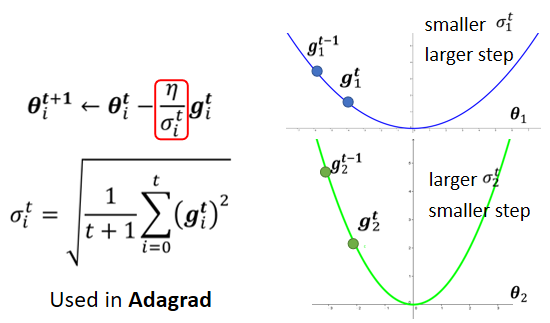
我们可以想像说，现在我们有两个参数：θᵢ¹和θᵢ²，θᵢ¹坡度小，θᵢ²坡度大，θᵢ¹因为它坡度小，所以你在θᵢ¹这个参数上面，算出来的gradient值都比较小，因为gradient算出来的值比较小，然后这个σ是gradient的平方和取平均再开根号，所以算出来的σ就小，所以learning rate就大，同理，θᵢ²会导致learning rate小。

但这种方法不能解决的是同一参数随时间变化的learning rate需求，他只是对每个参数做了不同的learning rate调整，但同一参数的gradient就会固定是差不多的值。

RMS Prop

RMS Prop这个方法,它的第一步跟Adagrad的方法,是一模一样的，但是它存有一个α，就像learning rate一样，这个你要自己调它，它是一个hyperparameter。

• α设很小趋近于0，就代表我觉得gᵢ¹相较于之前所算出来的gradient而言，比较重要。
• α设很大趋近于1，那就代表我觉得现在算出来的gᵢ¹比较不重要，之前算出来的gradient比较重要。

你用α来决定现在刚算出来的gᵢᵗ它有多重要，这个就是RMS Prop。他可以解决动态问题。

我们现在假设从这个地方开始：

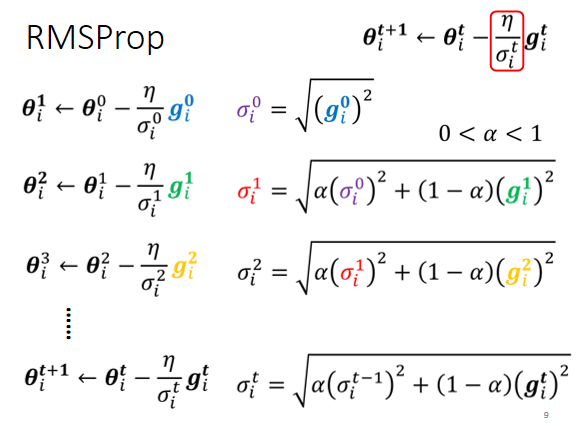
这个黑线是我们的error surface，从这个地方开始你要update参数，好你这个球就从这边走到这边，那因为一路上都很平坦，很平坦就代表说g算出来很小，代表现在update参数的时候，我们会走比较大的步伐。

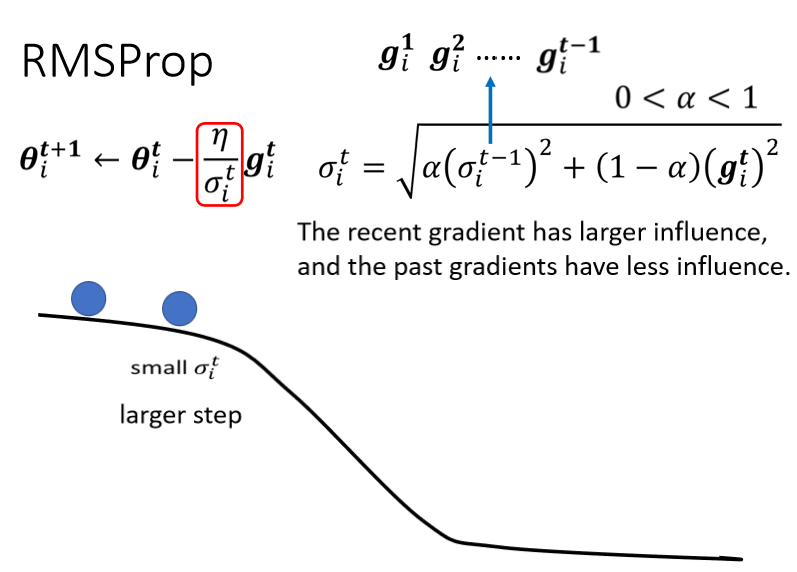
接下来继续滚，滚到这边以后我们gradient变大了，如果不是RMS Prop，原来的Adagrad的话它反应很慢，但如果你用RMS Prop，把α设小一点，让新的gradient影响比较大的话，那你就可以很快的让σ的值变大，于是可以很快的让你的步伐变小。
本来很平滑走到这个地方，突然变得很陡，那RMS Prop可以很快的踩一个刹车，把learning rate变小，如果你没有踩刹车的话，你走到这里这个地方，learning rate太大了，那gradient又很大，两个很大的东西乘起来，你可能就很快就飞出去了，飞到很远的地方。

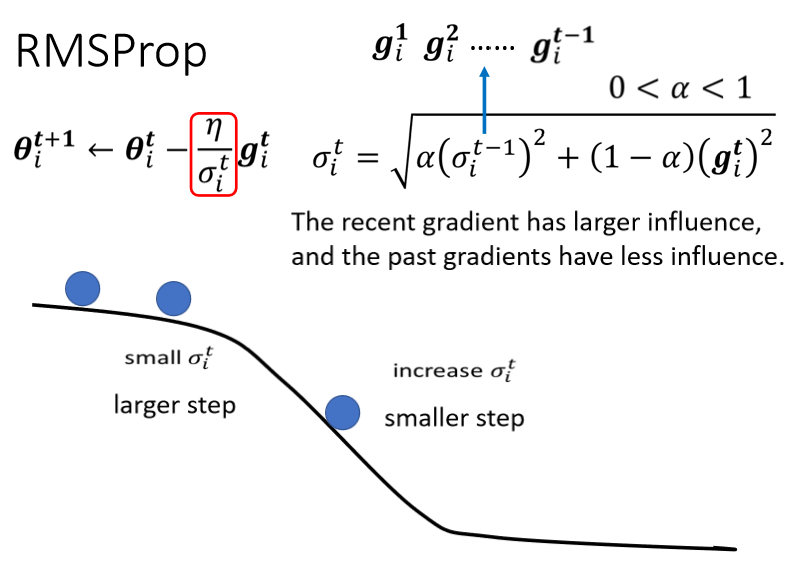
如果继续走，又走到平滑的地方了，因为这个σᵢᵗ你可以调整α，让它比较看重于最近算出来的gradient，所以你gradient一变小，σ可能就反应很快，它的这个值就变小了，然后你走的步伐就变大了。

Adam

实际上如今最常用的optimization的策略是Adam。

Adam就是RMS Prop加上Momentum，Adam的演算法跟原始的论文在这里

实际上adam在今天的pytorch里面已经集成，所以不用担心这种optimization的问题，optimizer这个deep learning的套件，往往都帮你做好了，然后optimizer里面，也有一些参数需要调，也有一些hyperparameter，需要人工决定，但是你往往用预设的，那一种参数就够好了，你自己调有时候会调到比较差的，往往直接复制pytorch里面Adam这个optimizer，然后预设的参数不要随便调，就可以得到不错的结果了，关于Adam的细节，如有兴趣，大家可以自己研究。

Learning Rate Scheduling

采用原始的adagrad，我们会得到如下：

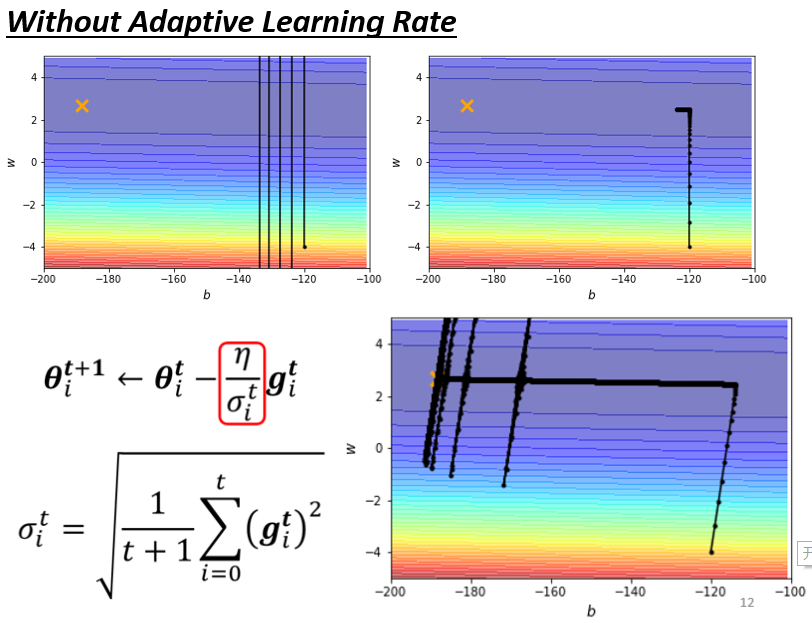
这个走下来没有问题，然后接下来在左转的时候，这边也是update了十万次，之前update了十万次，只卡在左转这个地方，现在有Adagrad以后，你可以再继续走到非常接近终点的位置，因为当你走到这个地方的时候，你因为这个左右的方向的，这个gradient很小，所以learning rate会自动调整，左右这个方向的，learning rate会自动变大，所以你这个步伐就可以变大，就可以不断的前进。

接下来的问题就是，为什么快走到终点的时候突然爆炸了呢？

我们在做这个σ的时候，我们是把过去所有看到的gradient，都拿来作平均

所以这个纵轴的方向，在这个初始的这个地方，gradient很大
可是这边走了很长一段路以后，这个纵轴的方向，gradient算出来都很小，所以纵轴这个方向，这个y轴的方向σ变小，小到一个地步以后，这个step就变很大，然后就爆炸了，爆炸以后没关系，有办法修正回来，因为出去以后，就走到了这个gradient比较大的地方，走到gradient比较大的地方以后，这个σ又慢慢的变大，σ慢慢变大以后，这个参数Update的步伐大小就慢慢的变小。

有一个方法可以解决这个问题，这个叫做learning rate scheduling（学习率调度）

我们刚才这边还有一项η,这个η是一个固定的值，learning rate scheduling的意思就是说，我们不要把η当一个常数，我们把它跟时间有关

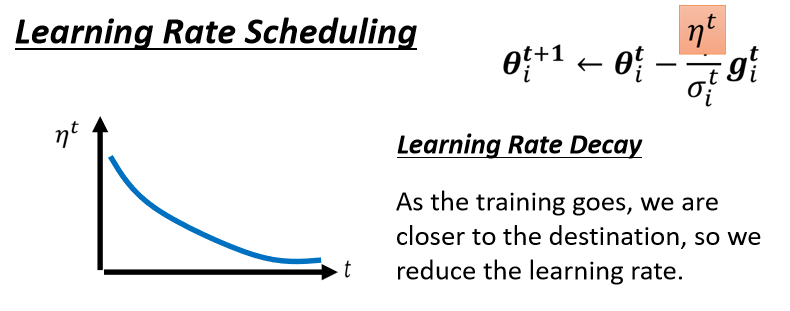
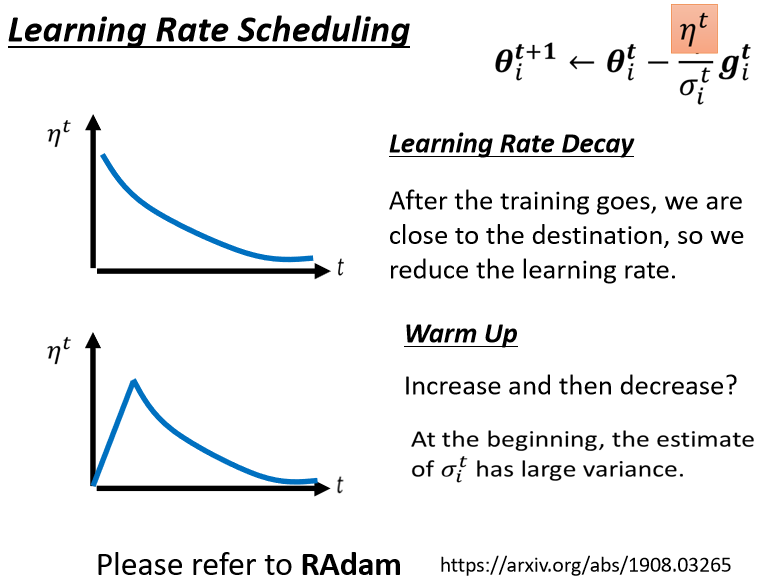
• 最常见的策略叫做Learning Rate Decay（学习率衰减），也就是说，随着时间的不断地进行，随着参数不断的update，我们这个η让它越来越小。
  这个就合理了，因为一开始我们距离终点很远，随着参数不断update，我们距离终点越来越近，所以我们把learning rate减小，让我们参数的更新踩了一个刹车，让我们参数的更新能够慢慢地慢下来，所以刚才那个状况，如果加上Learning Rate Decay有办法解决。

• 另外一个经典，常用的Learning Rate Scheduling的方式，叫做Warm Up（热身），Warm Up的方法是让learning rate，要先变大后变小，你会问说变大要变到多大呢，变大速度要多快呢，变小速度要多快呢，这个也是hyperparameter，要自己用手调的，但是大方向的大策略就是，learning rate要先变大后变小，这个黑科技出现在很多远古时代（2015）的论文里面，总之会让训练效果变得更好。

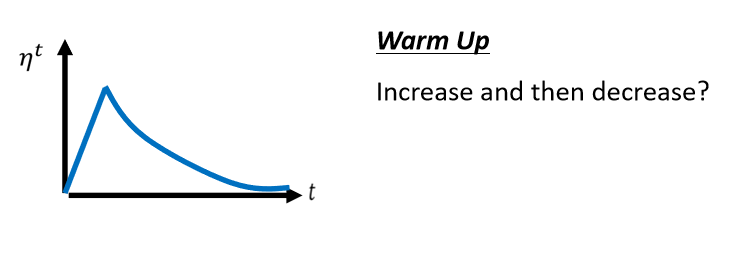
那为什么需要warm Up呢，这个仍然是今天可以研究的问题。

一个可能的解释是说，我们在用Adam，RMS Prop或Adagrad的时候，我们会需要计算σ,它是一个统计的结果，σ告诉我们，某一个方向它到底有多陡，或者是多平滑，那这个统计的结果，要看走狗i数据以后，这个统计才精准，所以一开始我们的统计是不精准的。

一开始我们的σ是不精准的，所以我们一开始不要让我们的参数，离初始的地方太远，先让它在初始的地方呢，做一些探索，所以一开始learning rate比较小，是让它探索收集一些有关error surface的情报，先收集有关σ的统计数据，等σ统计得比较精准以后，再让learning rate慢慢地爬升。

这是一个解释为什么我们需要warm up的可能性，如果你想要了解更多有关warm up的东西的话，可以看一篇paper，它是Adam的进阶版叫做RAdam，里面对warm up这件事情有更多的理解。

Summary of Optimization

从最原始的gradient descent进化到这一个版本：

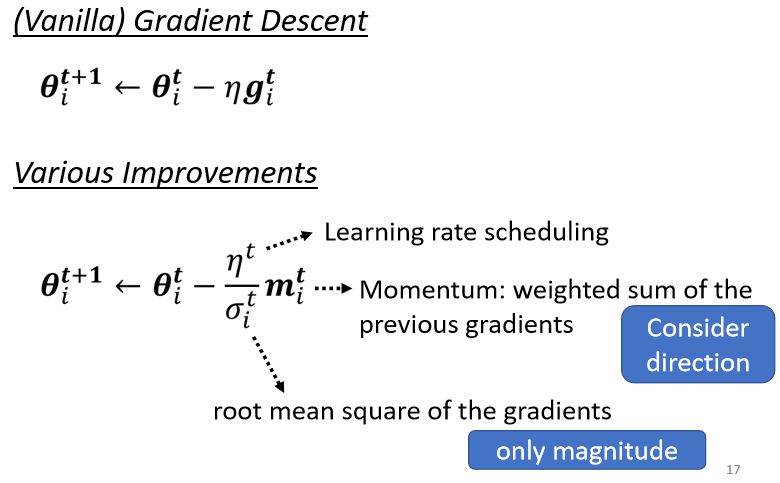
这个最终的版本里面有：

• Momentum，Update的方向，不是只考虑现在的Gradient，而是考虑过去所有Gradient的总和，
  针对Saddle Point或Local Minima的技术。
• Root Mean Square，动态控制update的步伐，平原峭壁任我行。
• Learning rate scheduling，宏观把控步伐的调整。

到目前为止，我们说的是当我们的error surface非常的崎岖，就像这个例子一样非常的崎岖的时候
我们用一些比较好的方法，来做optimization，前面有一座山挡着，我们希望可以绕过那座山，山不转路转。

有没有可能，直接把这个error surface移平，我们改Network里面的什么东西，改Network的架构activation function，或者是其它的东西，直接移平error surface，让它变得比较好train，也就是山挡在前面，就把山直接铲平的意思。

本文尚待回答的问题（后续文章更新）

• 如何“移山”