创作声明：主要为李宏毅老师的听课笔记，附视频链接：https://www.bilibili.com/video/BV1Wv411h7kN?p=15

前言

回答在optimization那篇笔记的问题，Batch Normalization（批归一化） 就是其中一个把山推平的想法。

假设有两个参数，它们对loss的斜率差别非常大，在w1这个方向上你的斜率变化很小，在w2这个方向上的斜率变化很大。

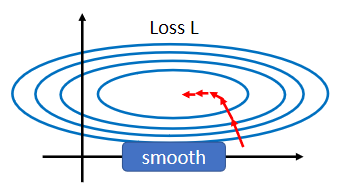
如果是固定的learning rate，可能很难得到好的结果，所以才需要adaptive learning rate、Adam等等比较进阶的optimization的方法，才能够得到好的结果。

现在从另外一个方向想，直接把难做的error surface改掉，看能不能够改得好做一点。

在做这件事之前，我们需要思考这种状况是怎么产生的？

假设现在有一个linear model，没有activation function，它的输入是x1跟x2 ，对应的参数是w1和w2。

当我们对w1有一个小小的改变，比如说加上delta w1的时候，L也会有一个改变，这是通过改变w1的时候改变了y，y改变的时候就改变了e，然后接下来就改变了L。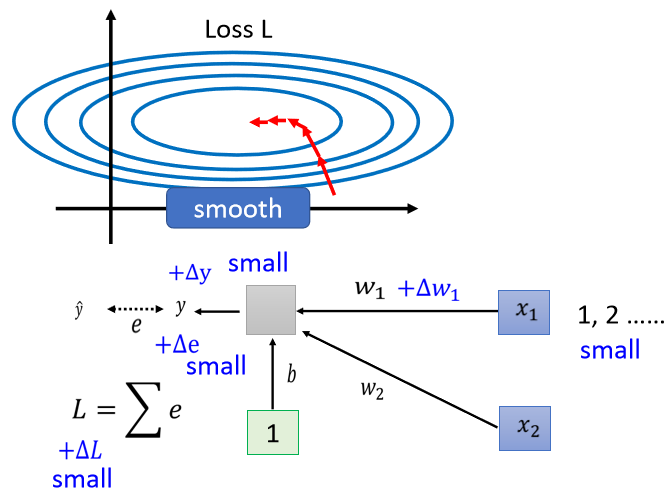

那什么时候w1的改变会对L的影响很小呢，也就是它在error surface上的斜率会很小呢？

当你的input很小的时候，假设x1的值在不同的training example里面它的值都很小，因为x1是直接乘上w1，如果x1的值很小，w1有变化的时候，它对y的影响也是小的，对e的影响也是小的，它对L的影响就会是小的。

反之，如果是x2，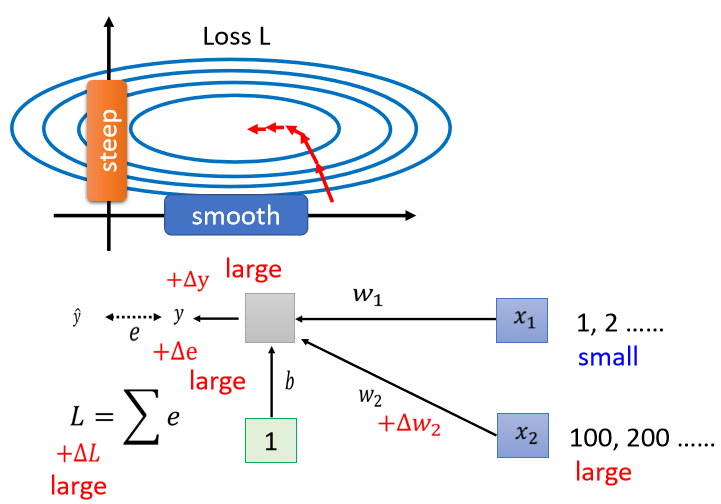

假设x2值偏大，它对L的影响也会是大的。

所以在这个linear model里面，当我们输入的feature的每一个dimension的值，它的scale差距很大的时候，我们就可能产生像这样子的error surface，就可能产生不同方向斜率非常不同，坡度非常不同的error surface。

所以我们有没有可能给feature里面不同的dimension，让它有同样的数值的范围？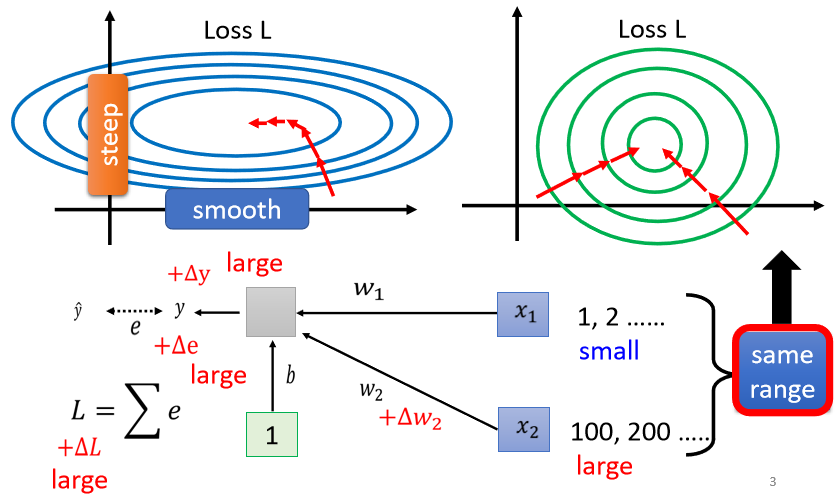

如果我们可以给不同的dimension同样的数值范围的话，那我们可能就可以制造比较好的error surface，让training变得比较容易一点。

其实有很多不同的方法，这些不同的方法，往往就合起来统称为Feature Normalization（特征归一化）

Feature Normalization

我们探讨Feature Normalization的一种可能性，它并不是Feature Normalization的全部。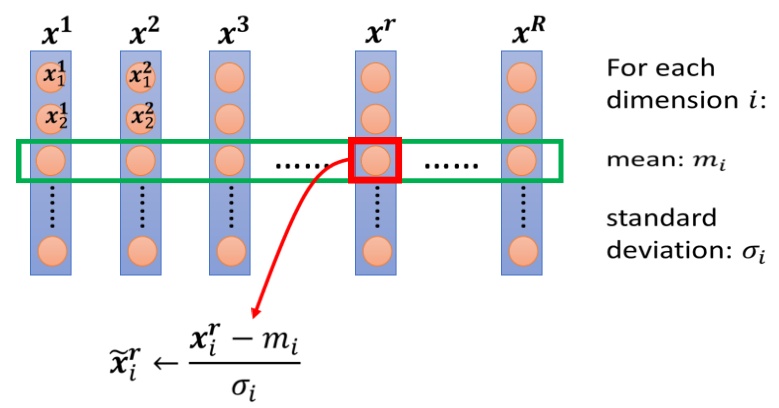

假设$x^1$到$x^R$，是我们所有的训练资料的feature vector（特征向量），
那我们把不同数据的feature vector，同一个dimension里面的数值取出来，然后去计算某一个dimension的mean（平均），它的mean就是$m_i$，我们计算第i个dimension的，standard deviation（标准差），我们用$\sigma_i$表示它,接下来我们就可以做一种normalization，那这种normalization叫做standardization(标准化），这边为了行文方便，暂时先都统称normalization。

我们是把某一个数值$x_i^r$，减掉这一个dimension算出来的mean，再除掉这个dimension，算出来的standard deviation，得到新的数值叫做$\widetilde{x}_i^r$
然后得到新的数值以后，再把新的数值代替原先的数值。

做完normalize以后有什么好处呢？

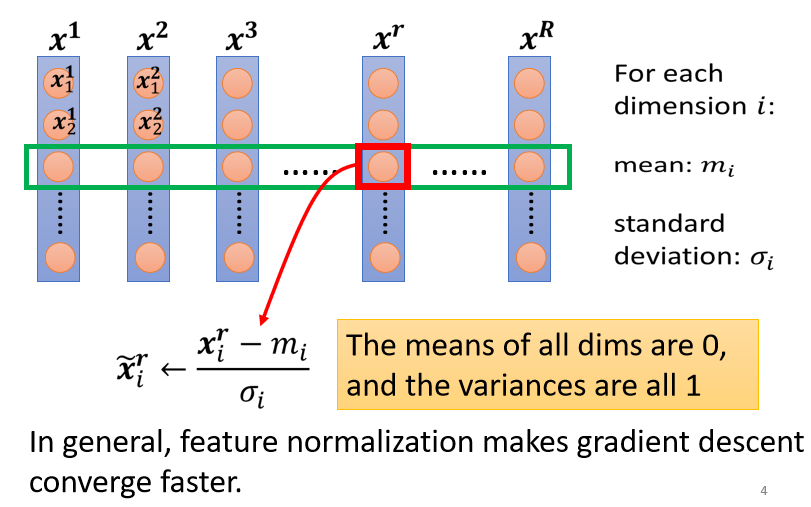
• 做完normalize以后，这个dimension上面的数值平均是0，然后它的variance（方差）就会是1，所以这一排数值的分布就都会在0上下。
• 对每一个dimension都做一样的normalization，就会发现所有feature不同dimension的数值都在0上下，那你可能就可以制造一个比较好的error surface。

所以Feature Normalization往往对你的training有帮助，它可以让你在做gradient descent的时候，这个gradient descent，它的Loss收敛更快一点，训练更顺利一点。

Considering Deep Learning

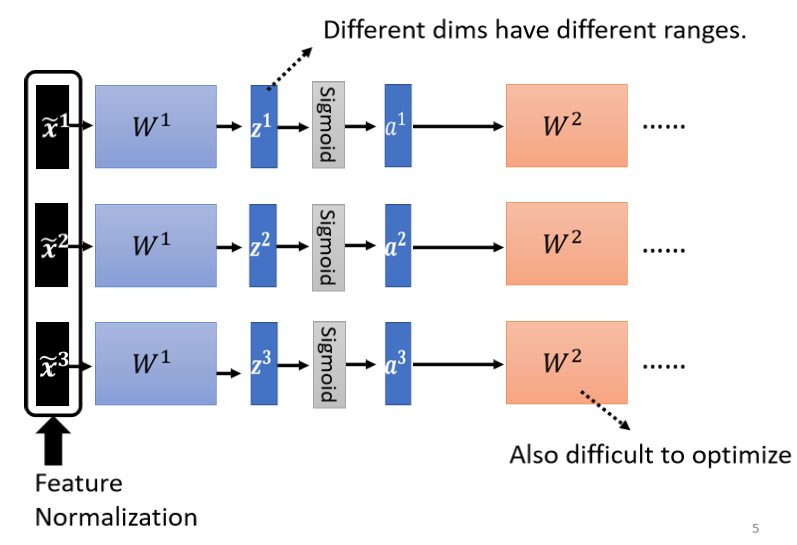
深度学习的神经网络会有很多层，如上图：

以$\widetilde{x}^1$为例，虽然它已经做 normalize 了,但是通过w1以后它就没有做 normalize，如果$\widetilde{x}^1$ 通过 w1得到是$z^1$，而 $z^1$不同的 dimension 间，它的数值的分布仍然有很大的差异的话，那我们要 train 第二层的参数，会不会也有困难呢？

对w2来说，这边的a或这边的z其实也是一种feature，我们应该要对这些feature也做normalization。

如果选择的是Sigmoid，那比较推荐对z做Feature Normalization，因为Sigmoid是一个s的形状，那它在0附近斜率比较大，所以如果你对z做Feature Normalization，把所有的值都挪到0附近，那你到时候算gradient的时候，算出来的值会比较大。

因为不一定是用sigmoid，所以不一定要把Feature Normalization放在z这个地方，如果是选别的，也许你选a也会有好的结果，在实际操作上，可能没有太大的差别、

这边对z做一下Feature Normalization。

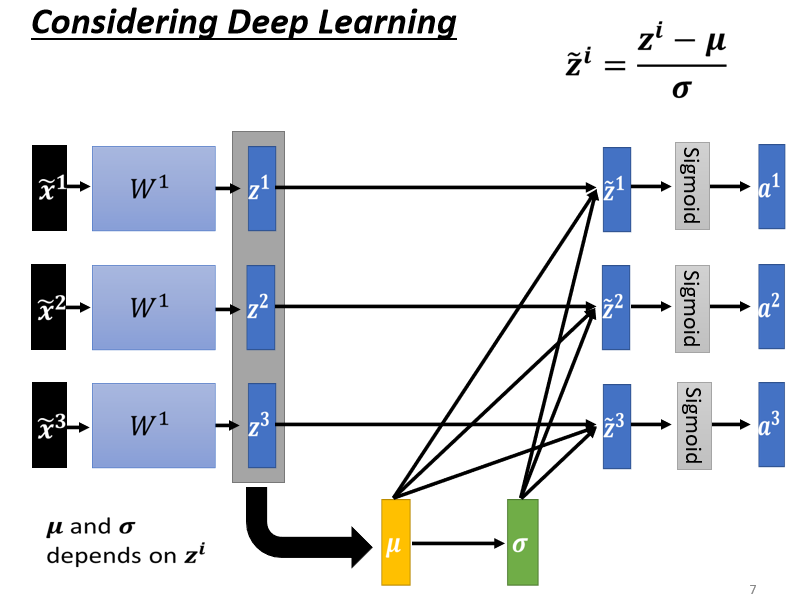
方法也是一样的，但是现在需要注意的是：

本来，如果我们没有做Feature Normalization的时候，改变$z^1$的值，只会改变这边$a^1$值，但是现在当你改变$z^1$的值的时候，$\mu$跟$\sigma$也会跟着改变，接着$z^2$的值$a^2$的值，$z^3$的值$a^3$的值，也会跟着改变。

所以之前，$\widetilde{x}^1$$\widetilde{x}^2$$\widetilde{x}^3$，它是独立分开处理的，但是在做Feature Normalization以后，这三个example，它们变得彼此关联了。

所以当你做Feature Normalization的时候，要把这一整个流程（就是收集一堆feature，把这堆feature算出$\mu$和$\sigma$这件事情）当做是network的一部分。

也就是说之前的network，每次都只有一个input，得到一个output，现在你有一个比较大的network，这个大的network，它是头一堆input，用这堆input在这个network里面，要算出$\mu$和$\sigma$，然后接下来产生一堆output。

那这边就会有一个问题，因为你的训练资料里面的data非常多，现在一个data set，benchmark corpus都上百万数据，GPU的内存没有办法，把所有data set的data都load进去。

在实际操作的时候，不会network考虑整个training data里面的所有example，只会考虑一个batch里面的example，举例来说，batch size设64，那network就是把64个data读进去，算这64个data的，算这64个data的，对这64个data都去做normalization。

因为我们在实际操作的时候我们只对一个batch里面的data，做normalization，所以这招叫做Batch Normalization。

这种Batch Normalization有一个问题就是，你一定要有一个够大的batch，你才算得出$\mu$和$\sigma$，假设batch size设1，那你就没有什么$\mu$和$\sigma$可以算。

所以这个Batch Normalization，是适用于batch size比较大的时候，因为batch size如果比较大，也许这个batch size里面的data就足以表示整个data set的分布，这个时候就可以，把这个本来要对整个data set，做Feature Normalization这件事情，改成只在一个batch上做Feature Normalization，作为approximation，

在做Batch Normalization的时候，往往还会有这样的设计：

算出$\widetilde{z}$以后，把这个$\widetilde{z}$与另外一个向量$\gamma$做element wise multiplication（直译为元素智能乘积，也就是两两做相乘）。
再加上向量$\beta$，得到$\hat{z}$，$\gamma$和$\beta$是network的参数，也是另外被learn出来的，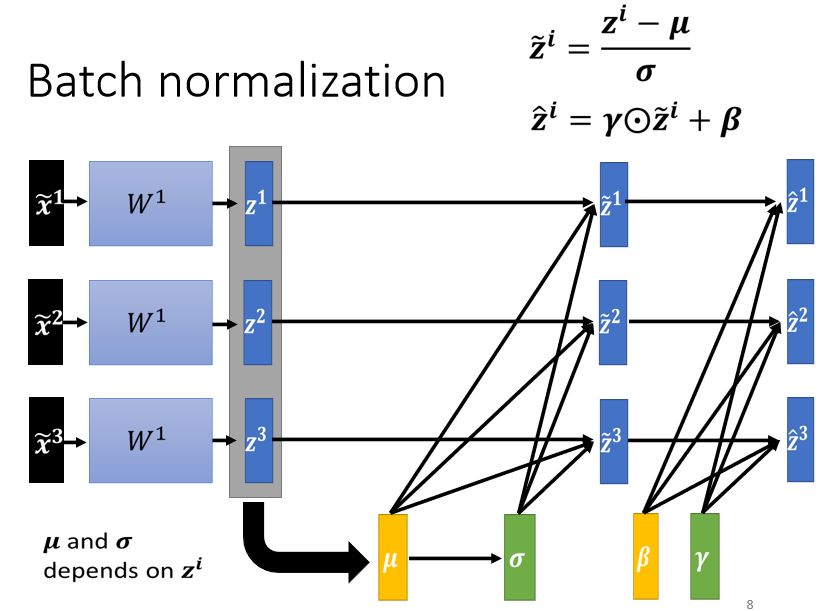

那为什么要加上$\gamma$和$\beta$的设计呢？

如果我们做normalization以后，那这边的$\widetilde{z}$的平均就一定是0，如果平均是0的话，就是给那network一些限制，那也许这个限制会带来什么负面的影响，所以我们利用$\gamma$和$\beta$让network自己去learn这个$\gamma$和$\beta$，来调整一下输出的分布。

可能有疑问是刚才说做Batch Normalization就是，为了要让每一个不同的dimension的range都一样，现在有$\gamma$和$\beta$的影响，会不会造成不同的dimension的range又不一样了？

有可能，但是你实际上在训练的时候，这个$\gamma$和$\beta$的初始的element分别是全是1和全是0，one vector和zero vector。

所以network在一开始训练的时候，每一个dimension的分布，是比较接近的，而当已经训练够长的一段时间，也许已经找到一个比较好的error surface，那再把$\gamma$和$\beta$调整好（来自实验经验的考虑确实会效果更好）。

Batch Normalization testing

在这里，testing有时候又叫inference。

为什么testing也要 normalization呢，不是直接test就好了嘛？
个人认为：神经网络在训练时候数据进行了归一化处理，而且引入相关学习的参数，那么本身归一化就是神经网络的一部分，他的参数也被学习到了。在testing的时候，自然也需要归一化。

在做Batch Normalization的时候，一个$\widetilde{z}$，也就是一个normalization过的feature进来，然后得到一个z，z要减掉$\mu$然后除$\sigma$，而$\mu$和$\sigma$是用一整个batch的资料算出来的。

如果今天是在做作业，一次有所有的testing的资料，确实也可以在testing的资料上面，制造一个一个batch。

但实际应用时可能是个在线问题，是一个真正的线上的app，要求尽快出结果，此时比如说你的batch size设64，我一定要等64个数据都进来，我才做运算吗，这显然是不行的，但是没有成batch，又没办法去算$\mu$和$\sigma$。

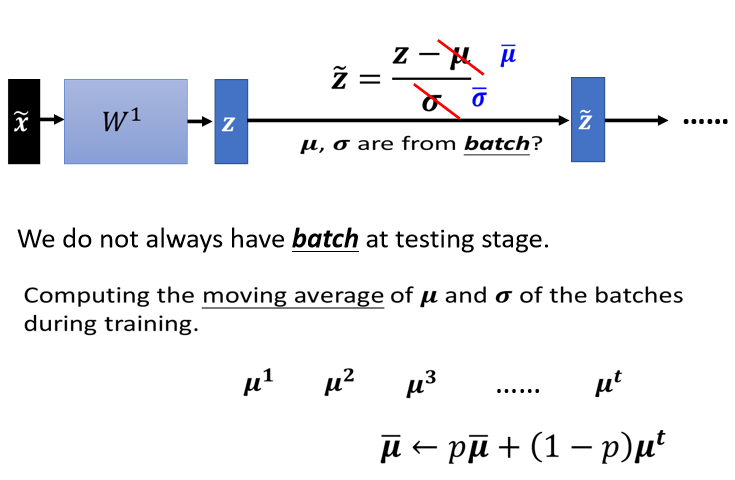
实际上的解法是这个样子的，如果看那个PyTorch的话，Batch Normalization在testing的时候，你并不需要做什么特别的处理，PyTorch帮你处理好了，处理的方法如下:

在training的时候，如果有做Batch Normalization的话，那么你每一个batch计算出来的$\mu$和$\sigma$都会拿出来算moving average（流动平均数）。

取第一个batch出来的时候，你就会算一个$\mu^1$，取第二个batch出来的时候，你就会算一个$\mu^1$，一直到取第t个batch出来的时候，你会算一个$\mu^t$，你会把你现在算出来的的一个平均值，叫做$\bar\mu$，乘上一个常数，这也是一个hyper parameter，也是需要调的。

在PyTorch里面，它设为0.1，然后加上(1-p)*$\mu^t$，然后来更新$\mu$的平均值，然后最后在testing的时候，你就不用算batch里面的$\mu$和$\sigma$。

因为testing的时候，在真正的application上，也没有batch这个东西，我们是直接拿$\bar\mu$和$\bar\sigma$来取代这边的$\mu$和$\sigma$，以上就是Batch Normalization在testing的时候的处理方法。

Batch Normalization的实际效果和原因猜想

实际效果

以下是从介绍Batch Normalization原始的paper上面截出来的一个实验结果，在原始的文件上还讲了很多其他的东西，举例来说有Batch Normalization用在CNN上要怎么用，更多的内容需要自己去读一下原始的文献：

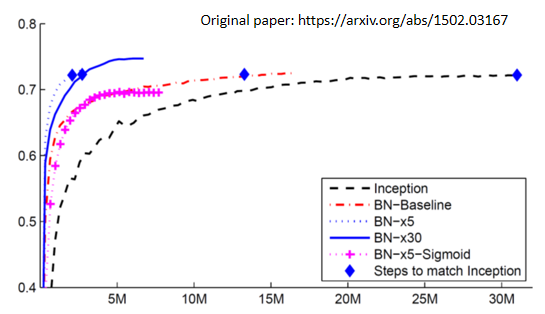
横轴代表的是训练的过程，纵轴代表的是validation set上面的accuracy。

黑色的虚线是没有做Batch Normalization的结果。

然后如果有做Batch Normalization，会得到红色的这一条虚线，红色这一条虚线，它训练的速度显然比黑色的虚线还要快很多，虽然最后收敛的结果只要给它足够的训练的时间，可能都跑到差不多的accuracy，但是红色这一条虚线，可以在比较短的时间内，就跑到一样的accuracy。这个蓝色的菱形，代表说这几个点的accuracy是一样的。

粉红色的线是sigmoid function，实际上我们一般都会选择ReLu，而不是用sigmoid function，因为sigmoid function它的training是比较困难的，但是这边想要强调的是，就算是sigmoid function它的training是比较困难的，加上Batch Normalization，还可以train的起来，图中没有sigmoid不做Batch Normalization的结果，因为在这个实验上，作者有说，sigmoid不加Batch Normalization，根本都train不起来。

蓝色的实线跟这个蓝色的虚线，是把learning rate设比较大一点，乘5和乘30，因为如果你做Batch Normalization的话，那error surface会比较平滑比较容易训练，所以可以把learning rate设大一点，这边不好解释的地方是不知道为什么learning rate设30倍的时候比5倍差，作者也没有解释，大家也都知道做deep learning就是有时候会产生不知道怎么解释的现象就是了，作者就是照实把他做出来的实验结果呈现在这个图上面。

原因猜想

接下来的问题就是，Batch Normalization为什么会有帮助呢？

在原始的Batch Normalization那篇paper里面，作者提出来一个概念，叫做internal covariate shift（内部协变量偏移），covariate shift（训练集和预测集样本分布不一致的问题就叫做“covariate shift”现象）这个词汇是原来就有的，internal covariate shift是Batch Normalization的作者自己发明的。

他认为说今天在train network的时候，会有以下这个问题：

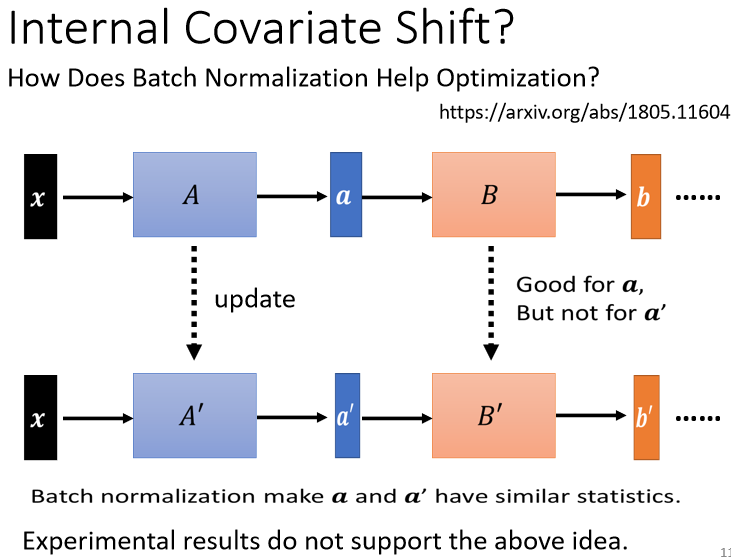
network有很多层，
x通过第一层以后得到a，
a通过第二层以后得到b，
计算出gradient以后，把A update成A′，把B这一层的参数update成B′
但是作者认为说，我们在计算B update到B′的gradient的时候，这个时候前一层的output是小a，那当前一层从A变成A′的时候，它的output就从a变成a′。

但是我们计算gradient的时候，我们是根据这个a算出来的啊，所以这个update的方向，也许它适合用在a上，但不适合用在a′上面，如果说Batch Normalization的话，我们会让a跟a′的分布比较接近，也许这样就会对训练有帮助。

但是有一篇paper叫做How Does Batch Normalization Help Optimization，就反驳了internal covariate shift的这一个观点
在这篇paper里面，他告诉你 internal covariate shift，首先它不一定是training network的时候的一个问题，然后Batch Normalization，它会比较好，也不见得是因为它解决了internal covariate shift。
在这篇paper里面呢，他做了很多的实验，比如说他比较了训练的时候a的分布的变化发现不管有没有做Batch Normalization，它的变化都不大。

然后他又说，就算是变化很大，对training也没有太大的伤害，接着他说，不管你是根据a算出来的gradient，还是根据a′算出来的gradient，方向都差不多。

所以他告诉你说，internal covariate shift，可能不是training network的一个主要问题，它可能也不是Batch Normalization会好的一个的关键，那有关更多的实验，读者可以自己参见这篇文章。

那为什么Batch Normalization会比较好呢，那在这篇How Does Batch Normalization Help Optimization这篇论文里面，他从实验上，也从理论上，至少支持了Batch Normalization，可以改变error surface，让error surface比较不崎岖这个观点。

所以这个观点是有理论的支持，也有实验的佐证的，在这篇文章里面，他还说如果我们要让network，这个error surface变得比较不崎岖，其实不见得要做Batch Normalization，感觉有很多其他的方法，都可以让error surface变得不崎岖，那他就试了一些其他的方法，发现说，跟Batch Normalization performance也差不多，甚至还稍微好一点，所以他就感叹
说，positive impact of batchnorm on training，可能是somewhat，serendipitous，什么是serendipitous呢，这个字眼可能可以翻译成偶然的，但偶然并没有完全表达这个词汇的意思，这个词汇的意思是说，你发现了一个什么意料之外的东西。

举例来说，盘尼西林就是意料之外的发现，盘尼西林的由来就是，弗莱明本来想要培养一些葡萄球菌，然后但是因为他实验没有做好，他的葡萄球菌被感染了，有一些霉菌掉到他的培养皿里面，然后他发现那些霉菌会杀死葡萄球菌，所以他就发现了盘尼西林，所以这是一种偶然的发现。

那这篇文章的作者也觉得，Batch Normalization也像是盘尼西林一样，是一种偶然的发现，但无论如何，它是一个有用的方法。

To learn more

其实Batch Normalization，不是唯一的normalization，normalization的方法有很多，那这边列举几个比较知名的方法：

Batch Renormalization
https://arxiv.org/abs/1702.03275

Layer Normalization
https://arxiv.org/abs/1607.06450

Instance Normalization
https://arxiv.org/abs/1607.08022

Group Normalization
https://arxiv.org/abs/1803.08494

Weight Normalization
https://arxiv.org/abs/1602.07868

Spectrum Normalization
https://arxiv.org/abs/1705.10941