Classification as Regression？

创作声明：主要为李宏毅老师的听课笔记。
正确的答案有加Hat，Model的输出没有加Hat

我们之前的笔记提到Regression就是输入一个向量，然后输出一个数值，那我们先思考一个问题，能不能用回归问题的解法去求解分类问题呢？

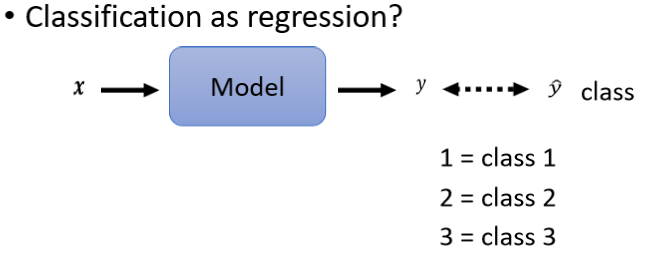
输入一个东西以后，我们的输出仍然是一个数值，它叫做y，然后y我们要让它跟正确答案，那个Class越接近越好，y是一个数字，我们怎么让它跟Class越接近越好呢，我们必须把Class也变成数字
举例来说Class1就是编号1，Class2就是编号2，Class3就是编号3，接下来呢我们要做的事情，就是希望y可以跟Class的编号，越接近越好。
但是这会是一个好方法吗，如果你仔细想想的话，这个方法也许在某些状况下，是会有瑕疵的。
因为当你用数字表示类别的时候，也就意味着数字上的联系也会代入到类别上的关系，

比如1和2的距离比1和3的距离近，但是类别上类别1和2就更相似吗？

显然不是。

Class as one-hot vector？

比较常见的做法是把Class用One-hot vector来表示，

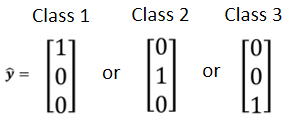
用One-hot vector来表示，就没有说Class1跟Class2比较接近，Class1跟Class3比较远这样的问题，如果用这个One-hot vector算距离的话，Class之间两两它们的距离都是一样。

如果我们今天的目标ŷ是一个向量，比如ŷ是有三个element的向量，那network也应该要Output三个维度。

我们过去做的都是Regression的问题，所以只Output一个数字，其实从一个数值改到三个数值，它是没有什么不同的，你可以Output一个数值，你就可以Output三个数值，所以把本来Output一个数值的方法，重复三次

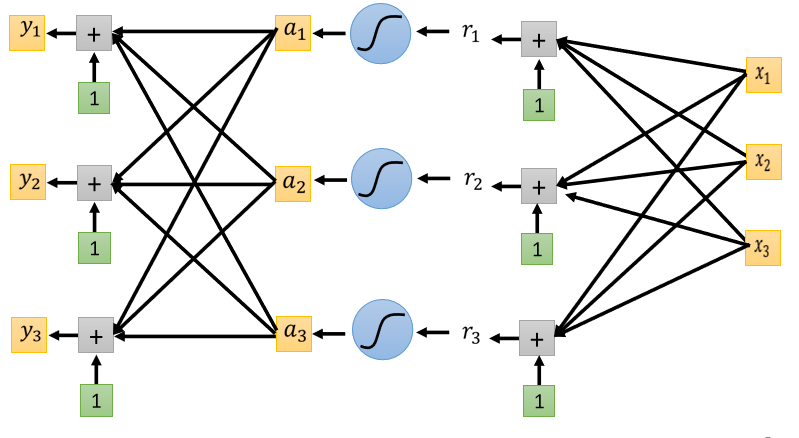
Classification with softmax

在做Classification的时候，我们往往会把y再通过一个叫做Soft-max的function得到$y^\prime$，然后我们才去计算$y^\prime$跟ŷ之间的距离。

为什么要加上Soft-max呢，一个比较简单的解释，一个骗小孩的解释就是，这个ŷ 它里面的值，都是0跟1，它是One-hot vector，所以里面的值只有0跟1，但是y里面有任何值。

既然我们的目标只有0跟1，但是y有任何值，我们就先把它Normalize到0到1之间，这样才好跟label的计算相似度，这是一个比较简单的讲法。

如果你真的想要知道，为什么要用Soft-max的话，你可以参考其他资料，如果你不想知道的话，你就记得这个Soft-max要做的事情，就是把本来y里面可以放任何值，改成挪到0到1之间。

Softmax
运行模式：

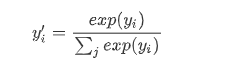
我们会先把所有的y取一个exponential，就算是负数，取exponential以后也变成正的，然后你再对它做Normalize，除掉所有y的exponential值的和，然后你就得到$y^\prime$。

或者是用图示化的方法是这个样子：

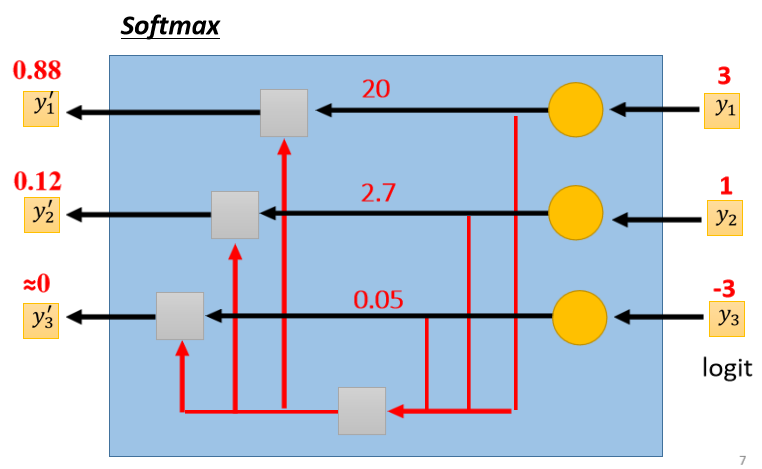
y₁取exp y₂取exp y₃取exp，把它全部加起来，得到一个Summation，接下来再把exp y₁’除掉Summation，exp y₂’除掉Summation，exp y₃’除掉Summation，就得到y₁’ y₂’ y₃’
有了这个式子以后，你就会发现

• y₁’ y₂’ y₃’，它们都是介于0到1之间
• y₁’ y₂’ y₃’，它们的和是1

举一个例子，本来y₁等于3，y₂等于1，y₃等于负3，exp3就是20，exp1就是2.7，exp -3就是0.05，做完Normalization以后，这边就变成0.88，0.12和0。
所以这个Soft-max它要做的事情，除了Normalized，让y₁’ y₂’ y₃’，变成0到1之间，还有和为1以外，它还有一个附带的效果是，它会让大的值跟小的值的相对差距更大，Soft-max的输入，往往就叫它logit。

Loss of Classification

我们把x丢到一个Network里面产生y以后，我们会通过soft-max得到y’，再去计算y’跟ŷ之间的距离，这个写作е。

计算y’跟ŷ之间的距离不只一种做法，举例来说，如果我可以让这个距离是Mean Square Error，但是更常用的做法，叫做Cross-entropy（交叉熵）

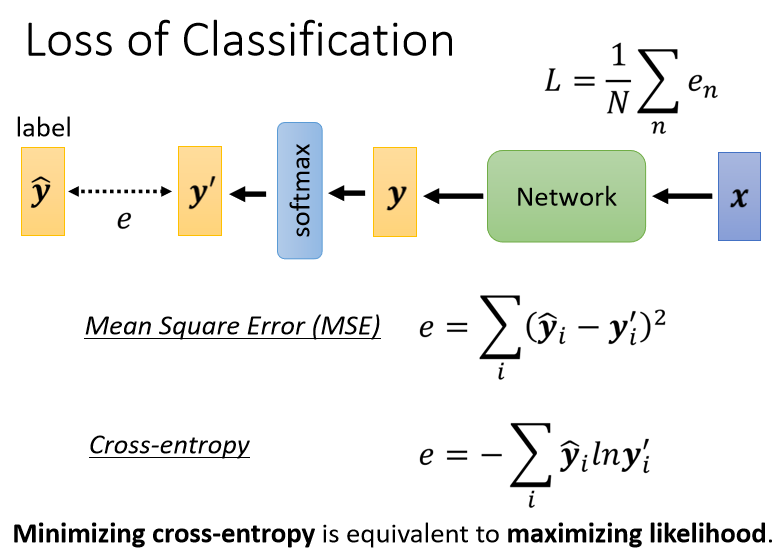
Cross-entropy是覆盖每一个值，把ŷ的第i位拿出来，乘上y’的第i位取Natural log,然后再全部加起来。

当ŷ跟y’一模一样的时候，MSE会是最小的，Cross-entropy也会是最小的。

Make Minimize Cross-entropy其实就是maximize likelihood。

实际上在pytorch里面，Cross-entropy跟Soft-max，他们是被绑在一起的，他们是一个Set，你只要Copy Cross-entropy，里面就自动内建了Soft-max。

我们从optimization的角度，来说明相较于Mean Square Error，Cross-entropy为什么被更常用在分类上（存在数学证明，有兴趣可以自行查阅）

对于一个3个Class的分类
Network先输出y₁y₂y₃，在通过soft-max以后，产生y₁’ y₂’跟y₃’
那接下来假设我们的正确答案是(1,0,0)，我们要去计算(1,0,0)这个向量，跟y₁’ y₂’跟y₃’他们之间的距离，这个距离我们用е来表示，е可以是Mean square error，也可以是Cross-entropy.
我们现在假设y₁是从-10到10，y₂是从-10到10，y₃我们就固定设成-1000。

因为y₃设很小，所以过soft-max以后y₃’就非常趋近于0，它跟正确答案非常接近，且它对我们的结果影响很少。
总之我们y₃设一个定值，我们只看y₁y₂有变化的时候，对我们的loss有什么样的影响。

进一步我们的目的是看损失函数设定为Mean Square Error，跟Cross-entropy的时候，算出来的Error surface会有什么不一样的地方，如下图：

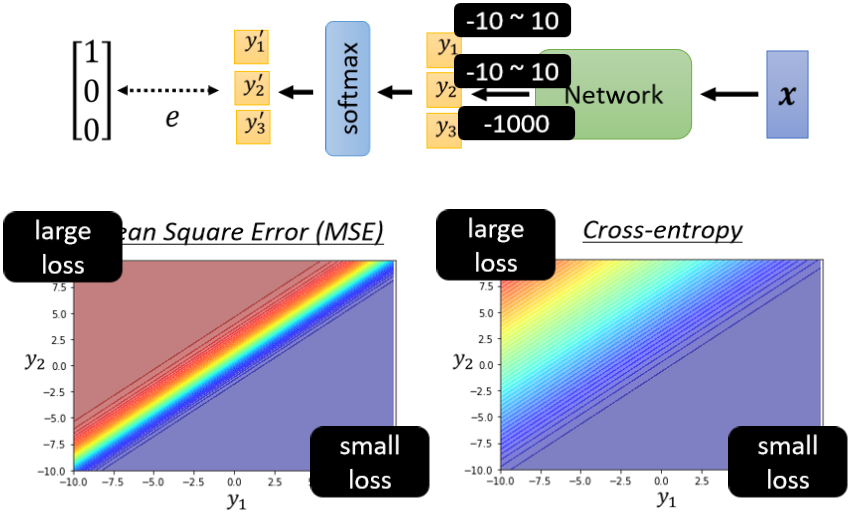
红色代表Loss大，蓝色代表Loss小，如果今天y₁很大y₂很小，就代表y₁’会很接近1，y₂’会很接近0，所以不管是对Mean Square Error，或是Cross-entropy而言，y₁大y₂小的时候Loss都是小的。

如果y₁小y₂大的话，这边y₁’就是0 y₂’就是1，所以这个时候Loss会比较大。

所以这两个图都是左上角Loss大，右下角Loss小，所以我们就期待最后在Training的时候，我们的参数可以走到右下角的地方。

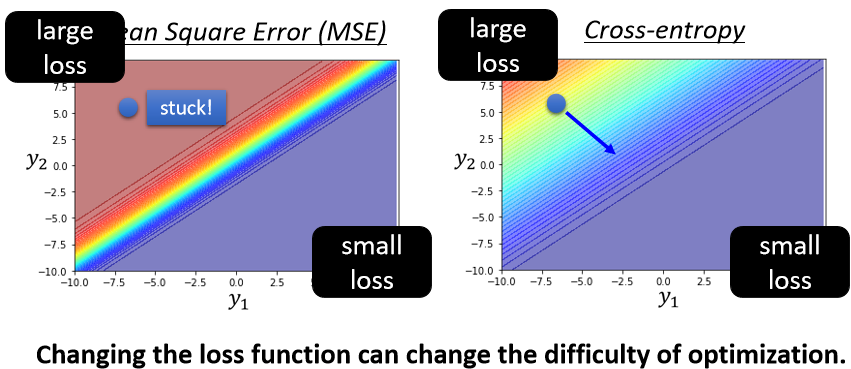
假设我们开始的地方都是左上角，如果我们选择Cross-Entropy，左上角有斜率，所以有办法通过gradient，一路往右下的地方走，如果选Mean square error的话就卡住了，Mean square error在这种Loss很大的地方，它是非常平坦的，它的gradient是非常小趋近于0的，如果你初始的时候在这个地方，离你的目标非常远，那它gradient又很小，你就会没有办法用gradient descent顺利的走到右下角的地方去。

所以如果在做classification，你选Mean square error的时候，你有非常大的可能性会train不起来，当然这个是在你没有好的optimizer的情况下，今天如果你用Adam，这个地方gradient很小，那gradient很小之后，它learning rate之后会自动帮你调大，也许你还是有机会走到右下角，不过这会让你的training，比较困难一点，让training的起步比较慢一点。

所以这也是一个很好的例子，告诉我们说，就算是Loss function的定义，都可能影响Training是不是容易这件事情，之前说BN把error surface炸平，这边也是一个好的例子告诉我们你可以改Loss function，同样可以改变optimization的难度。

本文尚待回答的问题

• softmax原理