创作声明：主要为李宏毅老师的听课笔记，附视频链接：https://www.bilibili.com/video/BV1Wv411h7kN?p=22

前言

CNN是Convolutional Neural Network（卷积神经网络） 的缩写，是专用于影像的神经网络。接下来的笔记将通过CNN的例子介绍Network的架构，它的设计有什么样的想法，为什么设计Network的架构可以让我们的Network结果做得更好。

从图像分类说起

我们要做图像的分类，也就是给机器一张图片，它要去决定这张图片里面有什么样的东西，那怎么做呢？

之前的笔记已经讲过怎么做分类这件事情，在以下的讨论里面，我们都假设我们的模型输入的图片大小是固定的，举例来说它固定输入的图片大小，都是100× 100的分辨率，就算是今天Deep Learning已经这么的Popular，我们往往都还是需要假设说，一个模型输入的图像大小都是一样的。

对于不同大小的图像，今天常见的处理方式是把所有图片都先Rescale成大小一样，再输入到图像辨识系统。

我们模型的目标是分类，所以我们会把每一个类别，表示成一个One-Hot的Vector，我的目标就叫做$\hat{y}$,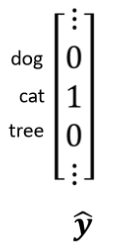

在这个One-Hot的Vector里面，假设我们现在类别是一个猫的话，那猫所对应的Dimension，它的数值就是1，其他的东西所对的Dimension的数值就是0，Dimension的长度决定了模型可以辨识出多少不同种类的东西，今天比较强的图像辨识系统，往往可以辨识出1000种以上的东西，甚至到上万种不同的Object，那如果你今天希望你的图像辨识系统，它可以辨识上万种Object，那你的Label就会是一个上万维，维度是上万的One-Hot Vector。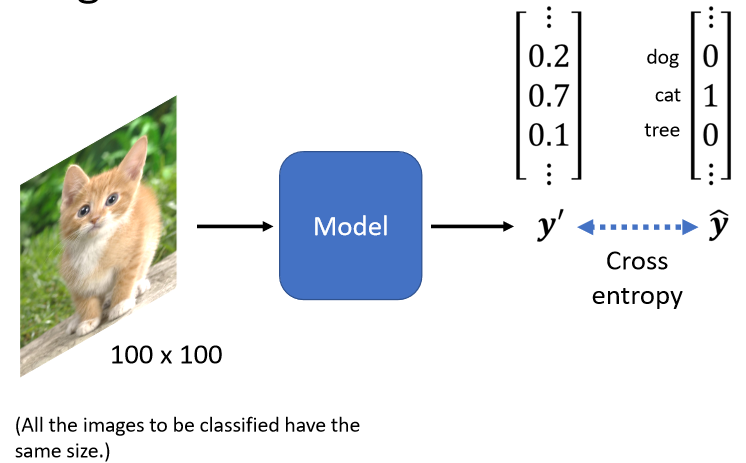

我们的模型的输出通过Softmax以后输出是$y\prime$，我们希望$y\prime$和$\hat{y}$的Cross Entropy越小越好。

图像的输入

接下来的问题是怎么把图像输入？

其实对于计算机来说，一张图片其实是一个三维的Tensor（张量），如果不知道Tensor是什么的话，你就认为它是维度大于2的矩阵就是Tensor，矩阵是二维，那超过二维的矩阵，你就叫它Tensor。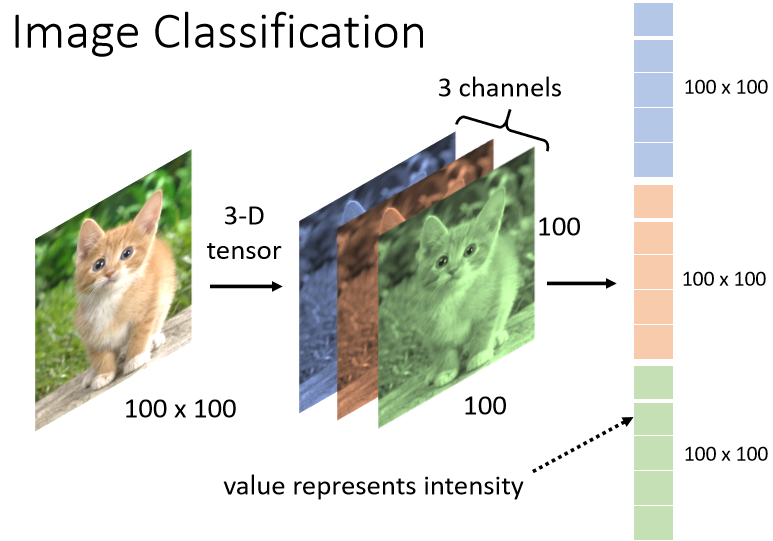

一张图片是一个三维的Tensor，其中一维代表图片的宽，另外一维代表图片的高，还有一维代表图片的Channel（通道）的数目。

一张彩色的图片每一个Pixel，都是由R G B三个颜色所组成的，所以这三个Channel就代表了R G B三个颜色，那长跟宽就代表了今天这张图片的分辨率，可以表示这张图片里面像素的数目。

到目前为止我们所说的Network的输入其实都是一个向量，所以我们只要能够把一张图片变成一个向量，我们就可以把它当做是Network的输入，但是怎么把这个三维的Tensor变成一个向量呢，最直觉的方法就是直接拉直它。

一个三维的Tensor里面有几个数字呢？

在这个例子里面有100×100×3个数字，把这些数字拿出来排成一排，就是一个巨大的向量，这个向量可以作为Network的输入，而这个向量里面，每一维它里面存的数值，其实就是某一个Pixel某一个颜色的强度，每一个Pixel由R G B三个颜色所组成。

之前的笔记的网络都是Fully Connected Network（全连接神经网络），如果我们把向量当做这种Network的输入，它的长度就是100×100×3，假设第一层的Neuron的数目有1000个，
每一个Neuron跟输入的向量的每一个数值都会有一个Weight，所以如果输入的向量长度是100×100×3，有1000个Neuron，第一层的Weight就有1000×100×100×3，也就是$3×10^7$，是一个非常巨大的数目。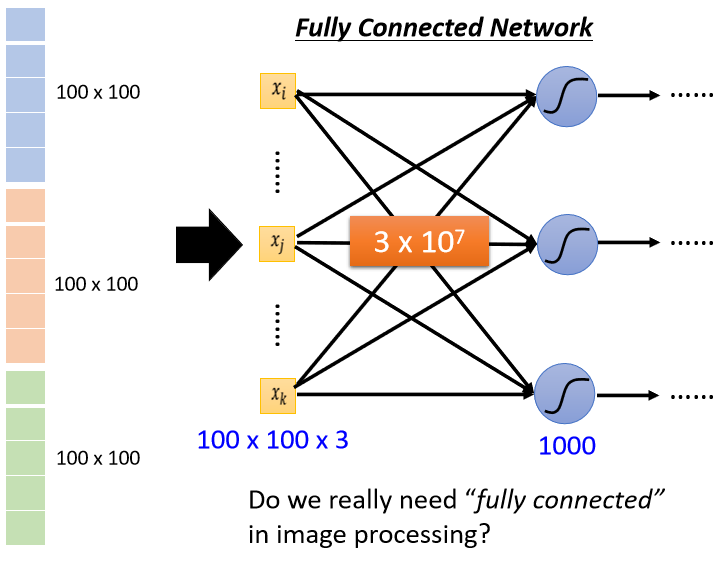

虽然随着参数的增加，我们可以增加模型的弹性，但是我们也增加了Overfitting的风险，有关模型的弹性，overfitting怎么产生的，这是相关的数学证明，总之概念上，如果模型的弹性越大越容易Overfitting。

在做图像辨识的时候，怎么避免使用这么多的参数，考虑到图像辨识这个问题本身的特性，其实我们并不一定需要Fully Connected，我们其实不需要每一个Neuron，跟Input的每一个Dimension都有一个Weight。

我们需要的是对图像辨识这个问题，对图像本身的特性的一些观察。

简化

第一个简化

观察

假设我们想要知道这张图片里面有一个鸟要怎么做呢？

对一个图像辨识的类神经网络里面的神经元而言，要做的就是侦测现在这张图片里面有没有出现一些特别重要的Pattern。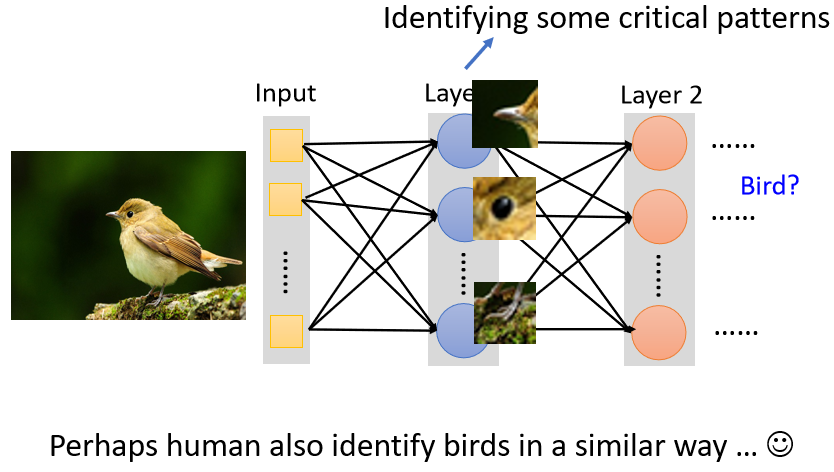

举例来说，有某一个Neuron，它看到鸟嘴这个Pattern，又有某个Neuron说，它看到眼睛这个Pattern
，又有某个Neuron说，它看到鸟爪这个Pattern。

类神经网络可以告诉你，因为看到了这些Pattern，所以它看到了一只鸟。
人类其实也是用同样的方法，来看一张图片中有没有一只鸟。

假设我们现在用Neuron做的事情就是判断说现在有没有某种Pattern出现，那我们并不需要每一个Neuron都去看一张完整的图片，因为这一些重要的Pattern，比如说鸟嘴比如说眼睛比如说鸟爪，并不需要看整张完整的图片，才能够得到这些信息，所以这些Neuron不需要把整张图片当作输入，它们只需要把图片的一小部分当作输入，就足以让它们侦测某些特别关键的Pattern有没有出现了。

根据这个观察，我们就可以做第一个简化。

简化

在CNN里面我们会设定一个区域叫做Receptive Field（感受野），每一个Neuron都只关心自己的Receptive Field里面发生的事情就可以

举例来说，你会先定义说这个蓝色的Neuron，它的守备范围就是这一个Receptive Field，那这个Receptive Field里面有3×3×3个数值，那对蓝色的Neuron来说，它只需要关心这一个小范围就好，不需要在意整张图片里面有什么东西。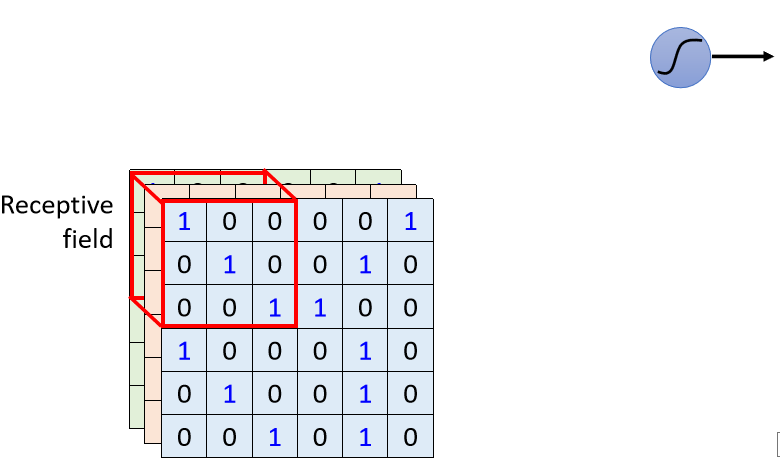

它要做的事情就是

1. 把这3×3×3的数值拉直，变成一个长度是3×3×3也就是27维的向量，再把这27维的向量作为这个Neuron的输入。
2. 这个Neuron会给27维的向量的，每一个Dimension一个Weight，所以这个Neuron有3×3×3 27个Weight。
3. 加上Bias得到的输出，这个输出再送给下一层的Neuron当作输入。
   
   每一个Neuron，它只考虑自己的Receptive Field，而Receptive Field要怎么决定要问你自己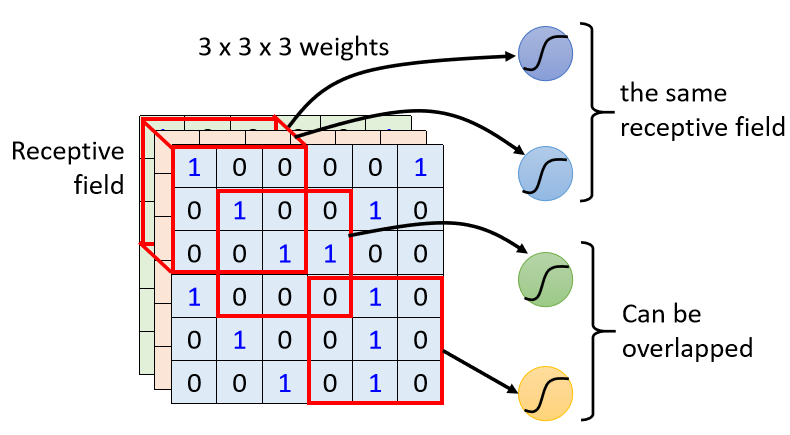
   
   你可以这么设定，这边有个蓝色的Neuron，它就看左上角这个范围，这是它的Receptive Field，另外又有另外一个黄色的Neuron，它是看右下角这个3×3×3的范围，Receptive Field彼此之间也可以是重叠的，比如说我现在画一个Receptive Field，那这个地方它是绿色的Neuron的守备范围，它跟蓝色的跟黄色的都有一些重叠的空间。

甚至可以两个不同的Neuron守备看到的范围是一样的，一个范围使用一个Neuron来守备可能没有办法侦测所有的Pattern，所以同个Receptive Field可以有多个不同的Neuron。

Receptive Field可以有大有小，可以只考虑某些channel，形状也可以是正方形长方形，如果说你要设计很奇怪的Receptive Field，去解决很特别的问题，那完全是可以的，这都是你自己决定的。

虽然Receptive Field可以任意设计，但也有最经典的Receptive Field的安排方式

1. 看所有的Channel

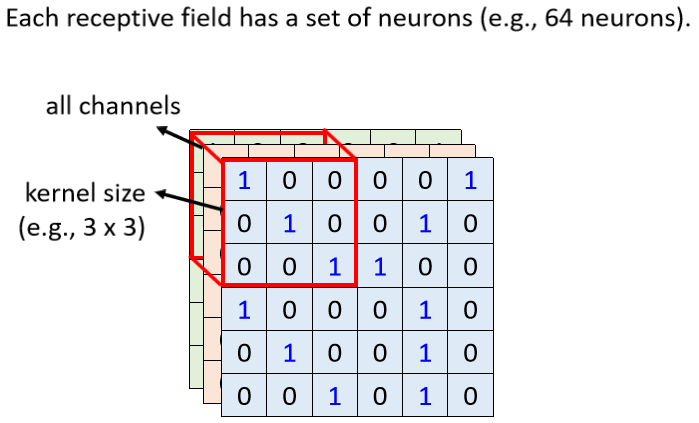
一般在做图像辨识的时候，可能不会觉得有些Pattern只出现某一个Channel里面，所以会看全部的Channel，所以既然会看全部的Channel

我们在描述一个Receptive Field的时候，只需要考虑他的宽和高，反正深度一定是考虑全部的Channel，而这个高跟宽合起来叫做Kernel Size（内核大小）。

举例来说，在这个例子里面，Kernel Size就是3×3，一般Kernel Size其实不会设太大，在图像辨识里面，往往做个3×3的Kernel Size就足够了，如果设个7×7和9×9，那已经算是大的Kernel Size。

如果Kernel Size都是3×3，意味着说我们觉得在做图像辨识的时候，重要的Pattern在3×3这么小的范围内，就可以被侦测出来了，可能会疑惑的是有些Pattern也许很大3×3的范围没办法侦测出来。

接下来的笔记会回答这个问题，现在需要先明白的是，常见的Receptive Field设定方式，就是Kernel Size 3×3，然后同一个Receptive Field，不会只有一个Neuron去关照它，往往会有一组一排Neuron去守备它，比如说64个或者是128个Neuron去守备一个Receptive Field的范围。
2. Stride

到目前为止，我们讲的都是一个Receptive Field，那不同Receptive Field之间的关系是怎么样呢？

举例：最左上角的这个Receptive Field，往右移一点就可以然后制造另外一个Receptive Field，这个移动的量叫做Stride（步）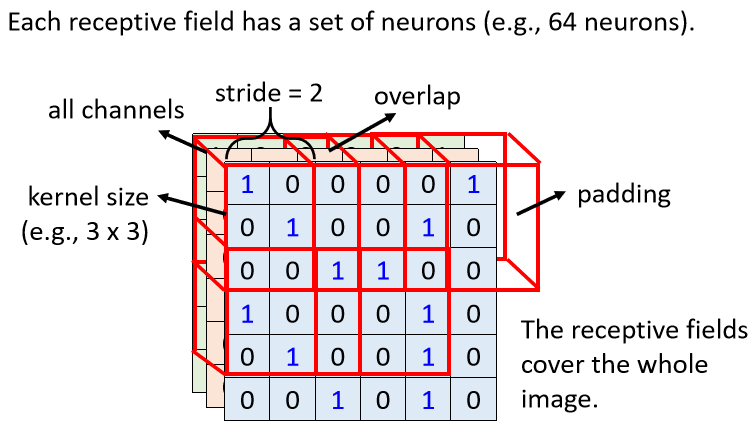

在这个例子里面Stride等于2，Stride是一个Hyperparameter，Stride你往往不会设太大，往往设1或2，因为你希望这些Receptive Field之间是有重叠的，因为假设Receptive Field完全没有重叠，那有一个Pattern就正好出现，在两个Receptive Field的交界上面，那就会变成没有任何Neuron去侦测它，那可能就会Miss掉这个Pattern，所以我们希望Receptive Field彼此之间有高度的重叠。

这边遇到一个问题，超出了图像的范围怎么办？

有人可能会说不要在这边摆Receptive Field，但这样就漏掉了图像的边缘，如果有个Pattern在图像的边缘，你就没有Neuron去关照那些Pattern，所以其实我们实际上中引入的方法是Padding（补值）。

比如今天Receptive Field有一部分，超出图像的范围之外了，那就当做那个里面的值都是0，其实也有别的补值的方法，Padding就是补值的意思，比如说有人会说我补整张图片里面所有Value的平均，或者你说，我把边缘的这些数字拿出来补，有各种不同的Padding的方法。
除了横着移动也有垂直方向上的移动，在这边我们一样垂直方向Stride也是设2，所以你有一个Receptive Field在这边，垂直方向移动两格，就有一个Receptive Field在这个地方，你就按照这个方式，扫过整张图片，所以整张图片里面，每个地方都被某一个Receptive Field覆盖，也就是图片里面每一个位置，都有一群Neuron在侦测那个地方有没有出现某些Pattern。

这是第一个简化Fully Connected Network的方式。
有人会疑问，如果我们只看一个感受野确实参数会少，但整个图片都扫一遍，考虑重叠现象，岂不是算起来参数更多？这就要提到第二个简化。

第二个简化

观察

同样的Pattern，它可能会出现在图片的不同区域里面，比如说鸟嘴这个Pattern，它可能出现在图片的左上角，也可能出现在图片的中间，虽然它们的形状都是一样的都是鸟嘴，但是它们可能出现在图片里面的不同的位置。

按照我们刚才的讨论，同样的Pattern出现在图片的不同的位置，也不是问题，因为出现在左上角的鸟嘴，它一定落在某一个Receptive Field里面，因为Receptive Field是移动完之后会复盖满整个图片的，所以图片里面没有任何地方不是在某个Neuron的守备范围内。

假设在Receptive Field里面，有一个Neuron的工作是侦测鸟嘴的话，那鸟嘴就会被侦测出来，所以就算鸟嘴出现在中间也没有关系，鸟嘴一定是在某一个Receptive Field的范围里面，那个Receptive Field一定有一组Neuron在照顾，如果其中有一个Neuron它可以侦测鸟嘴的话，那鸟嘴出现在图片的中间，也会被侦测出来。

问题是侦测鸟嘴的Neuron，它们做的事情其实是一样的，只是它们守备的范围是不一样，所以只要每个守备范围都放一个侦测鸟嘴的Neuron就不会遗漏了，问题是如果不同的守备范围，都要有一个侦测鸟嘴的Neuron，那参数量不会太多了吗？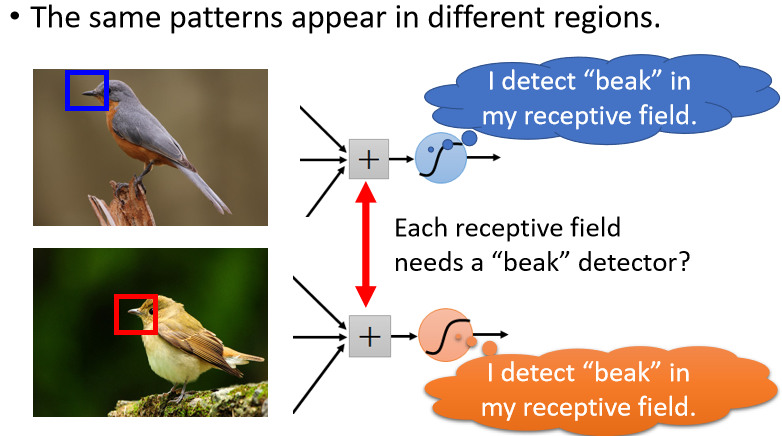

简化

我们实际的操作是让不同Receptive Field的Neuron共享参数，来削减参数量，也就是做Parameter Sharing（参数共享），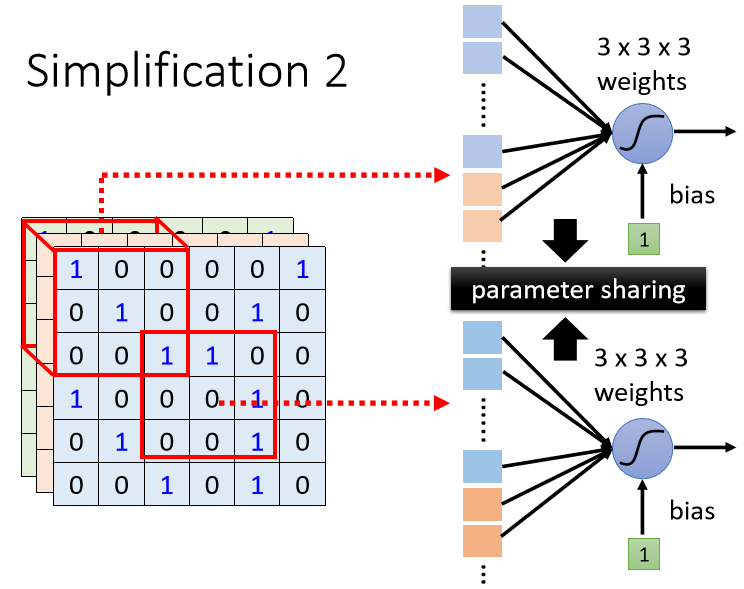

所谓共享参数就是这两个Neuron它们的weights完全是一样的，图中特别用颜色来标注它们的weights完全是一样的。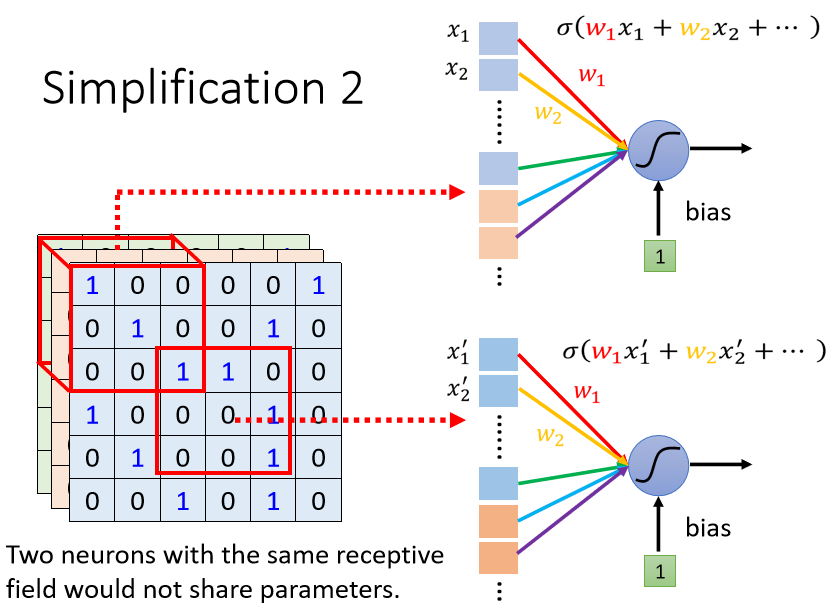

上面这个Neuron的第一个weight，叫做w1，下面这个Neuron的第一个weight也是w1，它们是同一个weight，用红色来表示。

上面这个Neuron的第二个weight是w2，下面这个Neuron的第二个weight也是w2，它们都用黄色来表示，以此类推……

总之上面这个Neuron跟下面这个Neuron，它们守备的Receptive Field是不一样的，但是它们的参数是一模一样的。

两个Neuron的参数一模一样，但是它们照顾的范围是不一样的，输入不一样，结果也不一样。

上面这个Neuron，我们说它的输入是，下面这个Neuron它的输入是，
上面这个Neuron的输出就是，x1×w1 + x2×w2，全部加加加再加Bias，然后透过Activation Function得到输出

下面这个Neuron虽然也有w1 w2，但w1跟w2是乘以x1’ x2’，所以它的输出不会跟上面这个Neuron一样。

我们让一些Neuron可以共享参数，至于要怎么共享，完全可以自己决定，而这个是你可以自己决定的事情，这里介绍的是常见的在图像辨识上面的共享的方法。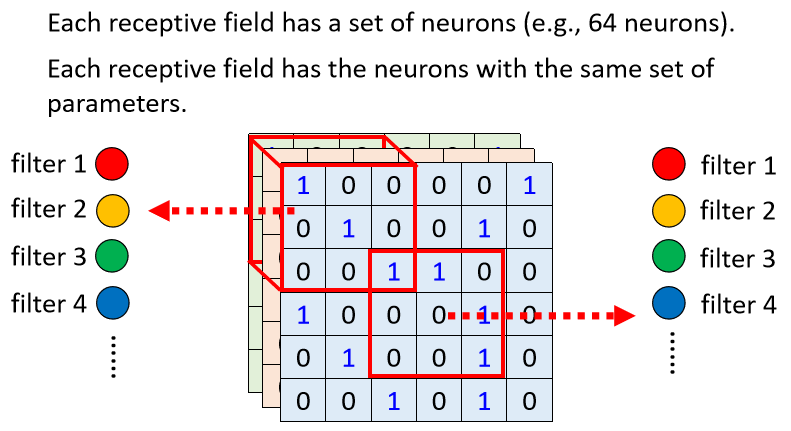

刚才提到每一个Receptive Field都有一组Neuron在负责守备，比如说有64个Neuron，所以左上这个Receptive Field有64个Neuron，右下这个Receptive Field也有64个Neuron，我们用一样的颜色，代表这两个Neuron共享一样的参数

左上边这个Receptive Field的第一个红色Neuron，会跟右下边这个Receptive Field的第一个红色Neuron共享参数，它的第二个橙色Neuron，跟右下边的第二个橙色Neuron共享参数，它的第三个绿色Neuron，跟右下边的第三个绿色Neuron共享参数，所以不同Receptive Field的同一neuron都只有一组参数而已，综合起来每个Receptive Field参数全都一致。

这些参数有一个名字，叫做Filter（过滤器），所以这两个红色Neuron，它们共享同一组参数，这组参数就叫Filter1，橙色这两个Neuron它们共同一组参数，这组参数就叫Filter2叫Filter3叫Filter4，以此类推。

Convolutional Layer

目前已经说了两个简化的方法，那我们来整理一下我们学到了什么，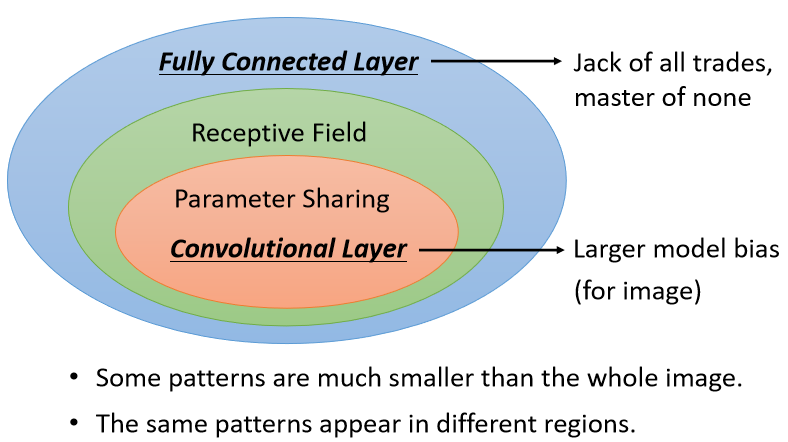

Fully Connected的Network是弹性最大的，但有时候不需要看整张图片，也许只要看图片的一小部分就可以侦测出重要的Pattern，所以我们有了Receptive Field的概念。
当我们强制一个Neuron只能看一张图片里面的一个范围的时候，它的弹性是变小的，如果是Fully Connected的Network，它可以决定看整张图片，还是只看一个范围，就如果它只想看一个范围，就把很多Weight设成0，就只看一个范围，所以加入Receptive Field以后，你的Network的弹性是变小的。

接下来是参数共享，参数共享进一步限制了Network的弹性，本来在Learning的时候，不同Receptive Field的同种Neuron可以各自有不同的参数，它们可以正好学出一模一样的参数，也可以有不一样的参数，但是加入参数共享以后，就意味着说某一些Neuron参数要一模一样，所以这又更增加了对Neuron的限制，而Receptive Field加上Parameter Sharing，就是Convolutional Layer（卷积层）。

有用到Convolutional Layer的Network，就叫Convolutional Neural Network（卷积神经网络），就是CNN，从这个图上你可以很明显地看出，其实CNN的的Model Bias比较大。

但Model Bias大，不一定是坏事，因为当Model Bias小，Model的Flexibility很高的时候，它比较容易Overfitting，Fully Connected Layer可以做各式各样的事情，它可以有各式各样的变化，但是它可能没有办法在任何特定的任务上做好。

而Convolutional Layer，它是专门为图像设计的，刚才讲的Receptive Field参数共享，这些观察都是为图像设计的，所以它在图像上仍然可以做得好，虽然它的Model Bias很大，但这个在图像上不是问题，但是如果它用在图像之外的任务，你就要仔细想想那些任务有没有我们刚才提到的图像任务中用的特性。

另外一种诠释方式

Filter

Convolutional的Layer就是里面有很多的Filter，这些Filter的大小是，3×3×Channel的Size，如果今天是彩色图片的话，那就是RGB三个Channel，如果是黑白的图片的话，它的Channel就等于1。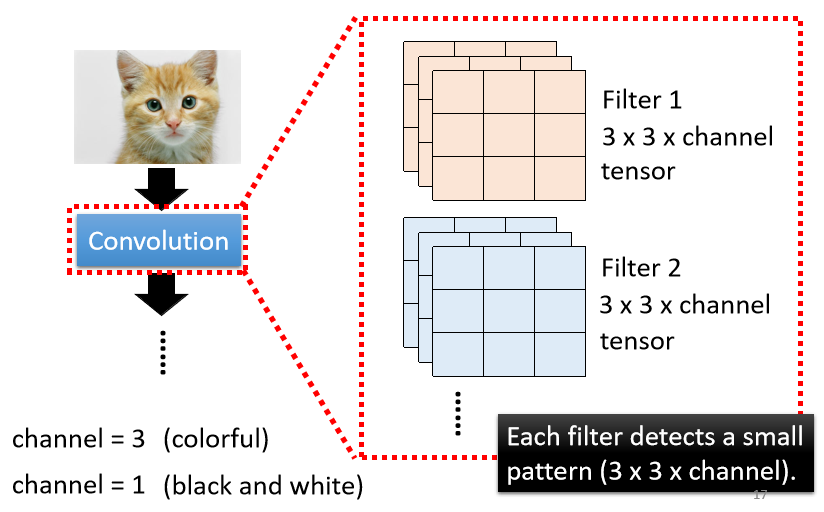

一个Convolutional的Layer里面就是有一排的Filter，每一个Filter都是一个3×3×Channel的Tensor。

Filter的作用就是要去图片里面探测某一个Pattern，当然这些Pattern，要在3×3×Channel那么小的范围内才能够被这些Filter抓出来

那这些Filter，怎么去图片里面抓Pattern的呢，我们现在举一个实际的例子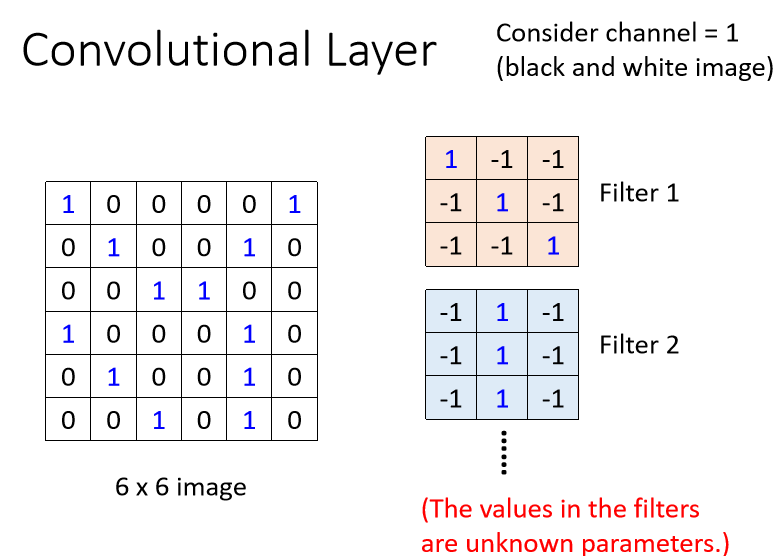

我们假设Channel是1，也就是说我们图片是黑白的图片

那我们假设这些Filter的参数是已知的，Filter就是一个一个的Tensor，这个Tensor里面的数值我们都已经知道了，（实际上这些Tensor里面的数值，其实就是Model里面的Parameter，这些Filter里面的数值其实是未知的，它是要通过gradient decent去找出来的）

不过我们现在已经假设这些Filter里面的数值已经找出来了，我们来看看这些Filter，是怎么跟一张图片进行运作，怎么去图片上面把Pattern侦测出来的。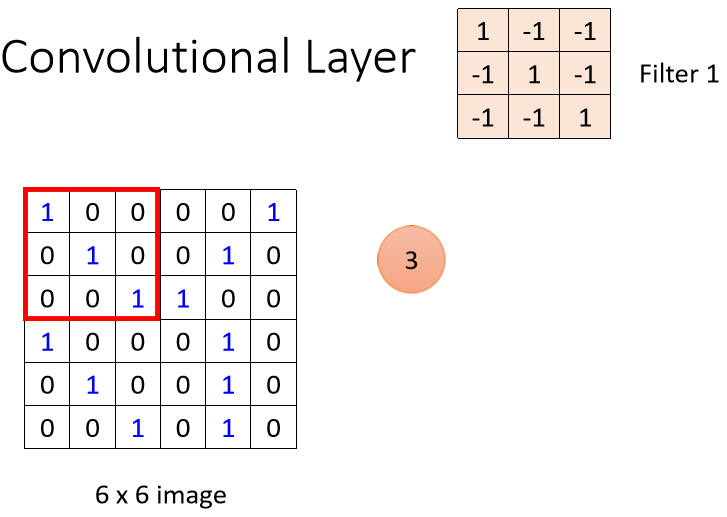

这是一个6×6的大小的图片，这些Filter的做法就是，先把Filter放在图片的左上角，然后把Filter里面所有的值，跟左上角这个范围内的9个值做相乘，也就是把这个Filter里面的9个值，跟这个范围里面的9个值呢，做Inner Product（内积），结果是3。（三通道无非体积对应内积，原理一样）

注意！在此处卷积运算中，内积不要理解为线性代数中矩阵的乘法，而是filter跟图片对应位置的数值直接相乘，所有的都乘完以后再相加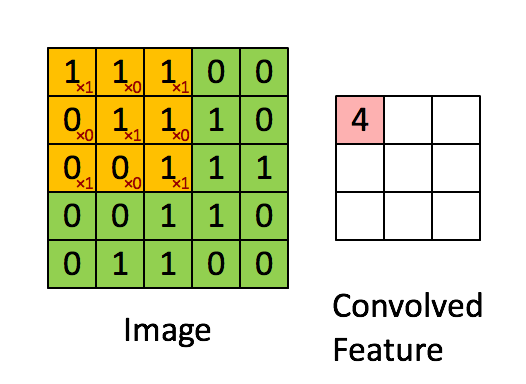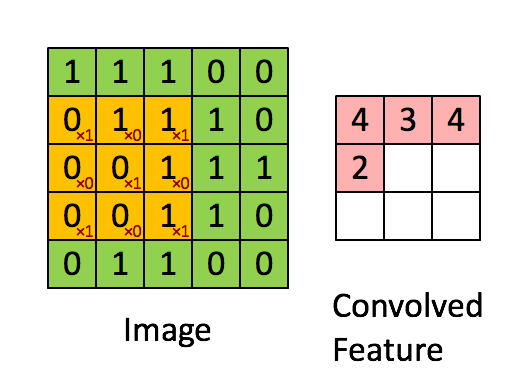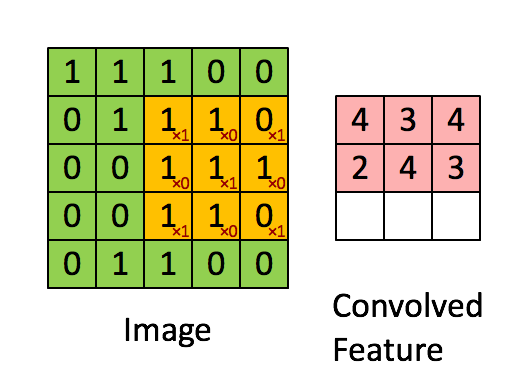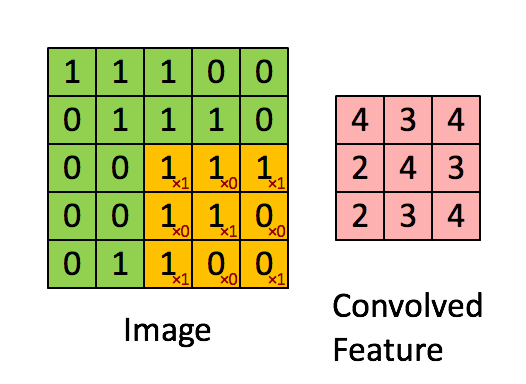

Filter本来放在左上角，接下来就往右移一点，那这个移动的距离叫做Stride。

在这里，我们Stride设为1，那往右移一点，然后再把这个Filter，跟这个范围里面的数值，算Inner Product算出来是-1，以此类推，再往右移一点再算一下，然后这边全部扫完以后，就往下移一点再算一下，一直到把这个Filter放在右下角。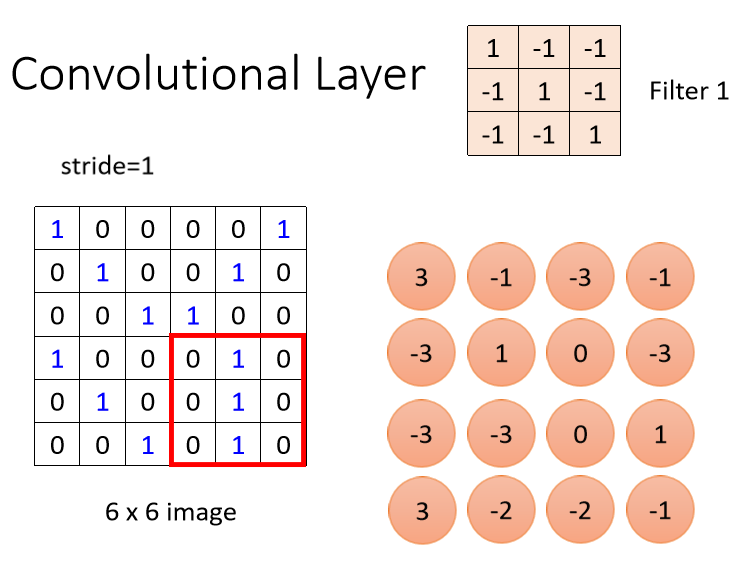

Feature Map

这个Filter怎么说它在侦测Pattern呢？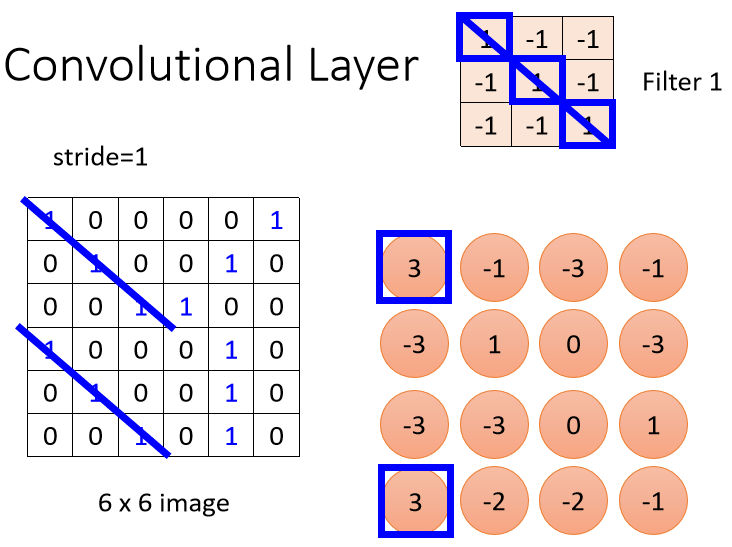

这个Filter里面，它对角线的地方都是1，所以它看到Image里面也出现连三个1的时候，它的数值会最大。
所以你会发现左上角和左下角的地方的值最大，就告诉我们说这个图片里面左上角和左下角有出现这个三个1连在一起的Pattern，这个是第一个Filter

接下来我们把每一个Filter，都做重复的Process，比如说这边有第二个Filter，我们就把第二个Filter，先从左上角开始扫起，得到一个数值，往右移一点再得到一个数值，再往右移一点再得到一个数值，反复同样的Process，反复同样的操作，直到把整张图片都扫完，我们又得到另外一群数值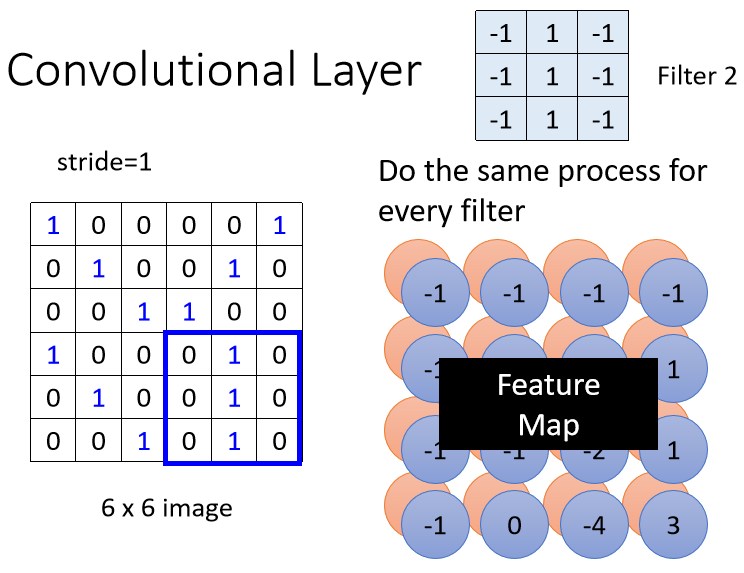

每一个Filter，都会给我们一群数字，红色的Filter给我们一群数字，蓝色的Filter给我们一群数字，如果我们有64个Filter，我们就得到64组的数字，而每一组数字都是Feature Map（特征图）的一个通道。

所以当我们把一张图片，通过一个Convolutional Layer，里面有64个Filter，产生出来64组数字，每一组在这个例子里面是4×4，他们叠在一起产生了Feature Map，你可以看成是另外一张新的图片，只是这个图片的Channel它有64个，这并不是RGB这个图片的Channel，在这里每一个Channel就对应到一个Filter，本来一张图片它三个Channel，通过一个Convolution，它变成一张新的图片有64个Channel。

Convolutional Layer可以叠很多层的，刚才是叠了第一层，那如果叠第二层的话，第二层的Convolution里面，也有一堆Filter，那每一个Filter呢，它的大小我们这边也设3×3，那它的高度必须设为64。

Filter的这个高度就是它要处理的图像的Channel，第一层的Convolution假设输入的图像是黑白的Channel是1，那我们的Filter的高度就是1，输入的图像如果是彩色的Channel是3，那Filter的高度就是3，那在第二层里面，我们也会得到一张图像，对第二个Convolutional Layer来说，它的输入也是一张图片，这个图片的Channel是64。

64是前一个Convolutional Layer的Filter数目，前一个Convolutional LayerFilter数目64，那输出以后就是64个Channel。

如果我们的Filter的大小一直设3×3，会不会让我们的Network，没有办法看比较大范围的Pattern呢？

其实不会的，如果我们在第二层Convolutional Layer，我们的Filter的大小一样设3×3的话，当我们看最左上角这个数值的时候，最左上角这个数值在原始图像上，其实是对应到这个范围，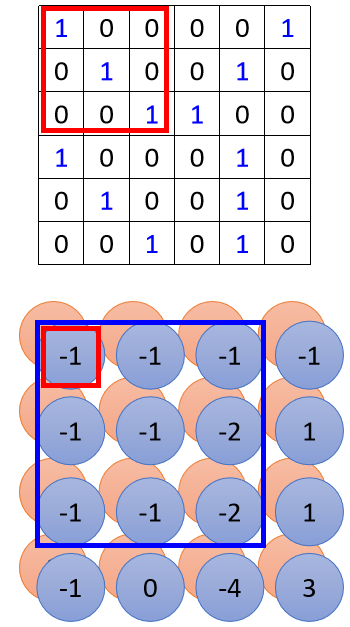

右下角的数值在原始图像上，其实是对应到这个范围，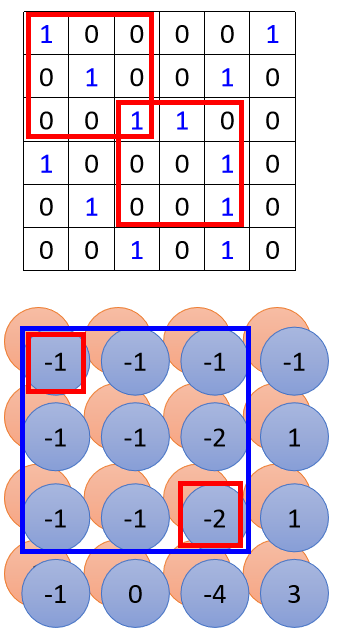

综合起来，我们在原来的图像上，其实是考虑了一个5×5的范围，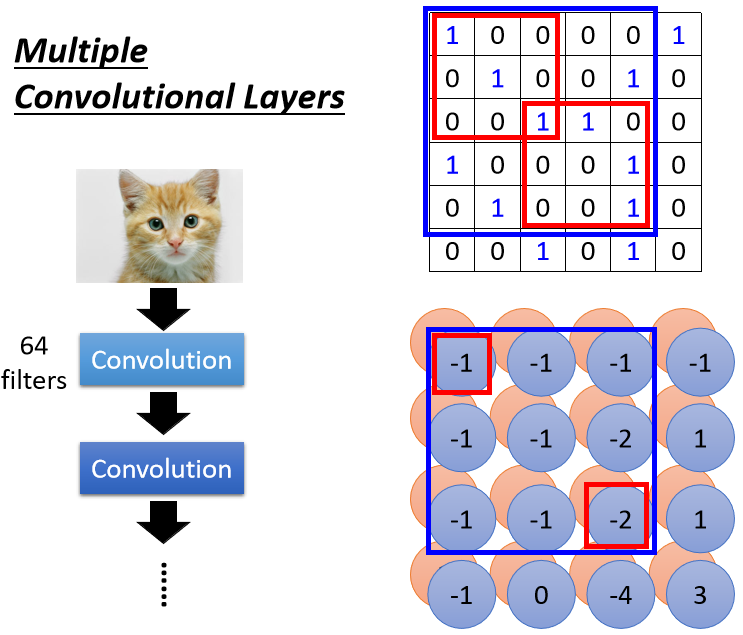

所以虽然我们的Filter只有3×3，但它在图像上考虑的范围是比较大的5×5，而今天你的Network叠得越深，同样是3×3的大小的Filter，它看的范围就会越来越大，所以Network够深，就不用怕侦测不到比较大的Pattern。

两个版本的总结

这两个版本的故事，是一模一样的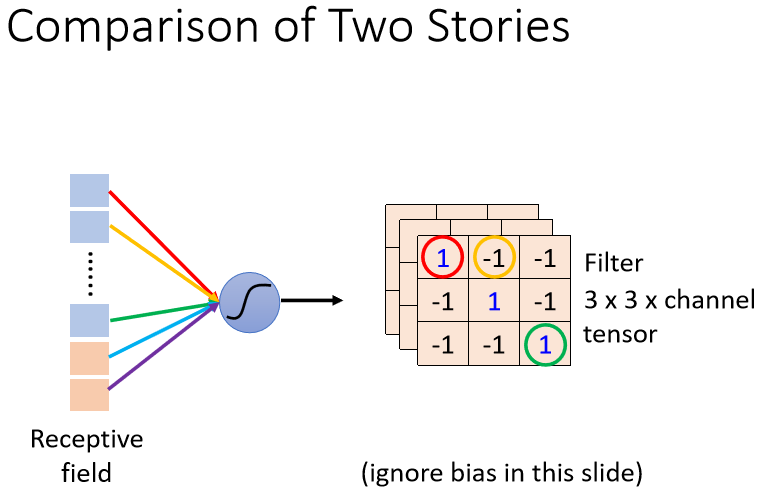

在第一个版本的故事里面，说到了Neuron会共享参数，这些共享的参数，就是第二个版本的故事里面的Filter

这个Filter里面有3×3×3个数字，这边特别用颜色把这些数字圈起来，意思是说这个Weight就是这个数字。

以此类推，这边把Bias去掉了，Neuron这个是有Bias的，这个Filter其实也有Bias，只是刚才没有提到，在实际操作中，CNN的这些Filter，其实都有Bias的数值。

把Filter扫过一张图片这件事其实就是Convolution。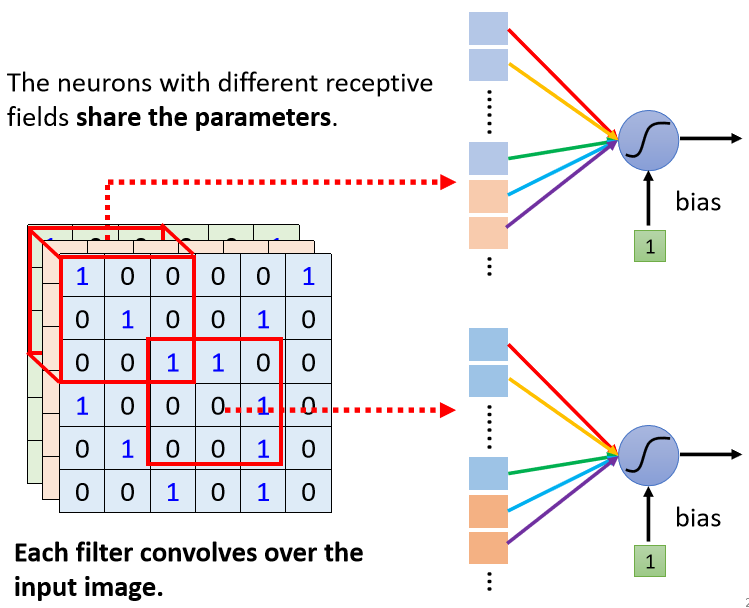

Pooling

Convolutional Layer，在做图像辨识时还有第三个常用的东西叫做Pooling（池化），

Pooling来自于另外一个观察，我们把一张比较大的图片做Subsampling（下采样），举例来说你把偶数的Column都拿掉，奇数的Row都拿掉，图片变成为原来的1/4，但是不会影响里面是什么东西，把一张大的图片缩小，这是一只鸟，这张小的图片看起来还是一只鸟

那所以有了Pooling这样的设计，Pooling本身没有参数，它里面没有Weight，它没有要Learn的东西，所以有人会说Pooling比较像是一个Activation Function，比较像是Sigmoid，ReLU那些，因为它里面是没有要Learn的东西的，它就是一个Operator，行为都是固定好的，没有要根据Data学任何东西。

Pooling也有很多不同的版本，我们这边讲的是Max Pooling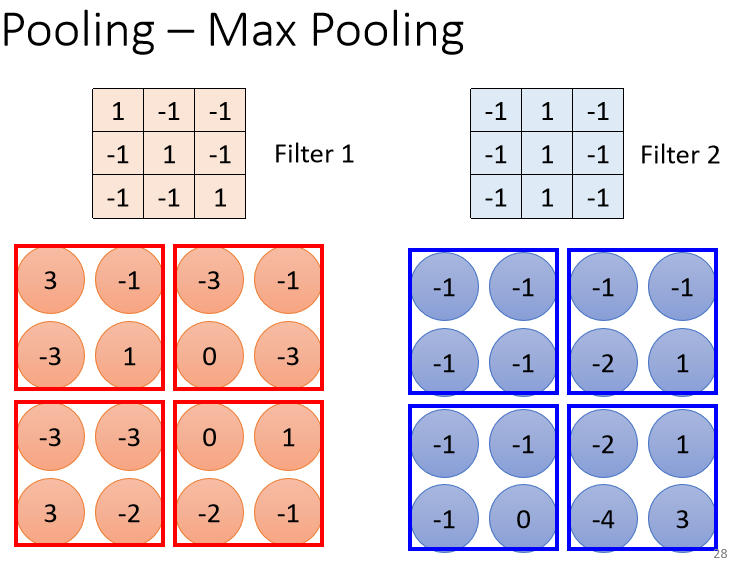

每一个Filter都产生一些数字，要做Pooling的时候，我们就把这些数字几个几个一组，比如说在这个例子里面就是2×2个一组，每一组里面选一个代表，在Max Pooling里面，我们选的代表就是最大的那一个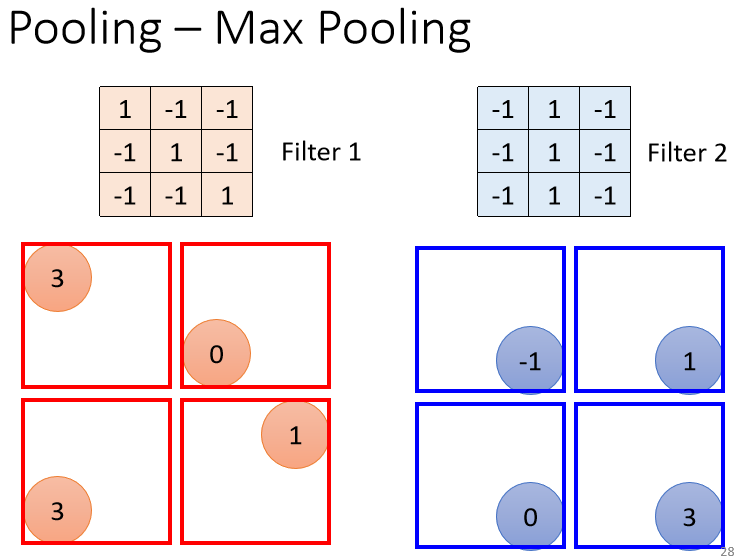

你不一定要选最大的那一个，这个自己可以决定的，Max Pooling这一个方法是选最大的那一个，但是也有average Pooling，还有选几何平均的，所以有各式各样的Pooling的方法
也不一定要2×2个一组，这个也是你自己决定的，你要3×3 4×4也可以。

所以我们做完Convolution以后，往往后面还会搭配Pooling，Pooling做的事情就是把图片变小，做完Convolution以后我们会得到一张图片，这一张图片里面有很多的Channel，那做完Pooling以后，我们就是把这张图片的Channel不变，本来64个Channel还是64个Channel，但是我们会把图片变得小一些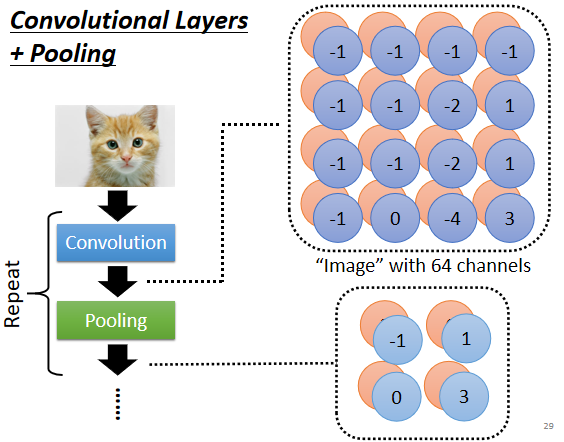

在刚才的例子里面，本来4×4的图片，如果我们把这个Output的数值2×2个一组，那4×4的图片就会变成2×2的图片，这个就是Pooling所做的事情

在实际操作中，往往是Convolution跟Pooling交替使用，就是可能做几次Convolution，做一次Pooling，比如两次Convolution一次Pooling。

不过预见的是Pooling对于Performance，还是可能会带来一点伤害的，因为假设你今天要侦测的是非常微细的东西，那做Subsampling，Performance可能会差一点

所以近年来你会发现，很多Network的设计，往往开始把Pooling丢掉，他会做Full Convolution的Neural Network，整个Network里面统统都是Convolution，完全不用Pooling

那是因为近年来运算能力越来越强，Pooling最主要的理由是为了减少运算量，做Subsampling，把图像变少减少运算量，如果你今天运算资源，足够支撑不做Pooling的话，很多Network的架构的设计往往就不做Pooling，，Convolution从头到尾，然后看看做不做得起来，看看能不能做得更好。

全连接

最后我们要做Flatten，Flatten的意思就是把这个图像里面本来排成矩阵的样子的数值拉直变成一个向量，再把这个向量放进进Fully Connected的Layer里面，最终你可能还要过个Softmax，然后得到图像辨识的结果，这就是一个经典的图像辨识的Network。如下图里面有Convolution，有Pooling有Flatten，最后再通过几个Fully Connected的Layer和Softmax，得到图像辨识的结果。

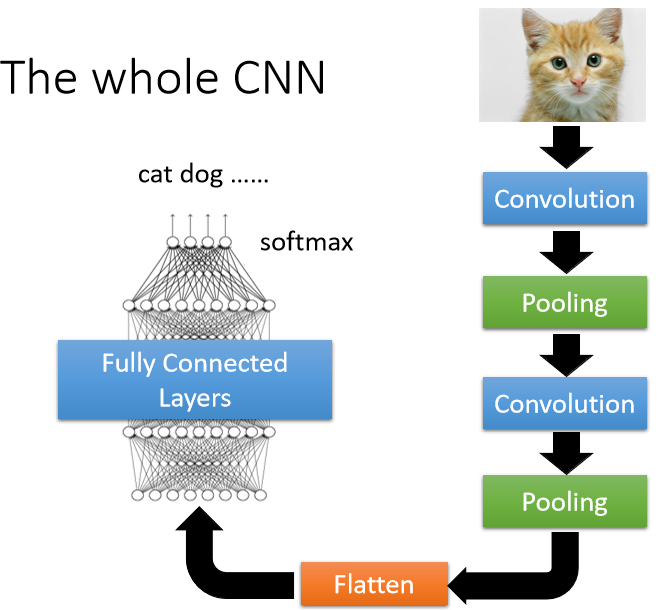
Flatten层用来将输入“压平”，即把多维的输入一维化，常用在从卷积层到全连接层的过渡。Flatten不影响batch的大小,有了全卷积网络之后 flatten已经不是必要操作。

为什么要放到全连接层呢？

前面的卷积本质还是在提取特征，而对特征图进行判断是全连接的事情。

全连接层（fully connected layers，FC）在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。在实际使用中，全连接层可由卷积操作实现：对前层是全连接的全连接层可以转化为卷积核为1x1的卷积；而前层是卷积层的全连接层可以转化为卷积核为hxw的全局卷积，h和w分别为前层卷积结果的高和宽（flatten的具体操作）。

但是大部分是两层以上，弹性更大，可以拟合更复杂的非线性函数。

目前由于全连接层参数冗余（仅全连接层参数就可占整个网络参数80%左右），一些一些性能优异的网络模型如ResNet和GoogLeNet等均用全局平均池化（global average pooling，GAP）取代FC来融合学到的深度特征，最后仍用softmax等损失函数作为网络目标函数来指导学习过程。需要指出的是，用GAP替代FC的网络通常有较好的预测性能。