创作声明：主要为李宏毅老师的听课笔记，附视频链接：https://www.bilibili.com/video/BV1Wv411h7kN?p=23

Sophisticated Input

之前的笔记提到的Network的Input都是一个向量，不管是在预测YouTube观看人数的问题上还是影像处理上，我们的输入都可以看作是一个向量，我们的输出，可能是一个数值，这个是Regression，可能是一个类别，这是Classification。

但假设我们遇到更复杂的问题，比如我们说输入是多个向量，而且这个输入的向量的数目是会改变的，或者我们刚才在讲图像识别的时候，还特别强调我们假设输入的图像大小都是一样的，那现在每次我们Model输入的Sequence的数目，Sequence的长度都不一样呢，那这个时候应该要怎么处理？这个问题就是Sophisticated Input（复杂信息输入）。

而Sophisticated Input的目的是什么呢？

假设我们今天要Network的输入是一个句子，每一个句子的长度都不一样，每个句子里面词汇的数目都不一样，

如果我们把一个句子里面的每一个词汇，都描述成一个向量，那我们的Model的输入，就会是一个Vector Set，而且这个Vector Set的大小，每次都不一样，句子的长度不一样，那你的Vector Set的大小就不一样。

把一个词汇表示成一个向量，最简单的做法是One-Hot的Encoding，

开一个很长很长的向量，这个向量的长度跟世界上存在的词汇的数目是一样多的，每一个维度对应到一个词汇，Apple就是100，Bag就是010，Cat就是001，以此类推。

但是这样的表示方法有一个非常严重的问题，它假设所有的词汇彼此之间都是没有关系的，从这个向量里面你看不到：Cat跟Dog都是动物所以他们比较接近，Cat跟Apple一个动物一个植物，所以他们比较不相像。这个向量里面，没有任何这些关系的信息。

有另外一个方法叫做Word Embedding（单词嵌入），如果将word看作文本的最小单元，可以将Word Embedding理解为一种映射，其过程是：将文本空间中的某个word，通过一定的方法，映射或者说嵌入（embedding）到另一个数值向量空间。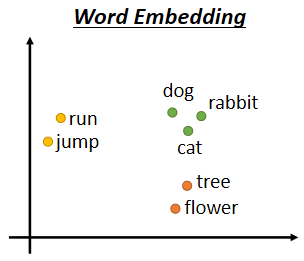

这个向量具有语义的信息，如果把Word Embedding画出来的话，你会发现，所有的动物可能聚集成一团，所有的植物可能聚集成一团，所有的动词可能聚集成一团。

What is the output？

输入可以是一堆向量，那这个时候，我们有可能有什么样的输出呢，有三种可能性：

1. 每一个向量都有一个对应的Label
   当你的模型，看到输入是四个向量的时候，它就要输出四个Label，而每一个Label，它可能是一个数值，那就是Regression的问题，如果每个Label是一个Class，那就是一个Classification的问题。

举例来说在文字处理上，假设你今天要做的是POS Tagging（词性标注），你要让机器自动决定每一个词汇它是什么样的词性，它是名词还是动词还是形容词等等。

这个任务其实并不容易，举例来说，你现在看到一个句子，I saw a saw.并不是“我看一个看”，而是“我看到一个锯子”，这个第二个saw当名词用的时候，它是锯子，所以机器要知道第一个saw是个动词，第二个saw虽然它也是个saw，但它是名词。

这个任务输入跟输出的长度是一样的，这个就是属于第一个类型的输出。
2. 一整个Sequence，只需要输出一个Label
举例来说，Sentiment Analysis（情感分析），Sentiment Analysis就是给机器看一段话，它要决定这段话是正面的还是负面的。

假设你的公司开发了一个产品，这个产品上线了，你想要知道网友的评价怎么样，但是你又不可能一则一则网友的留言都去分析，那可以用Sentiment Analysis的技术，让机器自动去判断当一则贴文里面有提到某个产品的时候，它是正面的还是负面的，这个是Sentiment Analysis，给一整个句子，只需要一个Label，Positive或Negative，这个就是第二类的输出
。
3. 计算机自己决定应该要输出多少个Label
我们不知道应该输出多少个Label，机器要自己决定，应该要输出多少个Label，可能你输入是N个向量，输出可能是N’个Label，为什么是N’，机器自己决定，这种任务又叫做sequence to sequence的任务。翻译就是sequence to sequence的任务，因为输入输出是不同的语言，它们的词汇的数目本来就不会一样多。

今天先拿第一种情况举例。

Sequence Labeling

输入跟输出数目一样多的状况又叫做Sequence Labeling，你要给Sequence里面的每一个向量，都给它一个Label，那要如何处理Sequence Labeling的问题呢？

直觉的想法是我们就用Fully-Connected Network，虽然这个输入是一个Sequence，但我们就各个击破，不要管它是不是一个Sequence，把每一个向量，分别输入到Fully-Connected的Network里面，然后Fully-Connected的Network就会给我们输出。

那这么做显然有非常大的瑕疵，假设今天是词性标记的问题，给机器一个句子，I saw a saw，对Fully-Connected Network来说，后面这一个saw跟前面这个saw完全一模一样，它们是同一个词汇，既然Fully-Connected的Network输入同一个词汇，它没有理由输出不同的东西，但实际上，你期待第一个saw要输出动词，第二个saw要输出名词，但对Network来说它不可能做到，因为这两个saw明明是一模一样的，你叫它一个要输出动词，一个要输出名词，它完全不知道要怎么处理。

所以有没有可能让Fully-Connected的Network，考虑更多的信息，比如说上下文这样的信息呢？

这是有可能的，把前后几个向量都串起来，一起丢到Fully-Connected的Network就结束了，让它可以考虑一些跟我现在要考虑的这个向量相邻的其他向量的新鞋，但是真正的问题，但是如果今天我们有某一个任务，不是考虑一部分就可以解决的，而是要考虑一整个Sequence才能够解决的话，那要怎么办呢？

有人可能会说这个很容易，把Window开大一点然后把整个Sequence盖住就结束了，但是今天Sequence的长度是有长有短的，我们输入给我们的Model的Sequence的长度，每次可能都不一样，那你可能要统计一下你的训练数据，然后看看你的训练数据里面，最长的Sequence有多长，然后开一个Window比最长的Sequence还要长，你才有可能把整个Sequence盖住。

但是你开一个这么大的Window，意味着Fully-Connected Network，它需要非常多的参数，不只运算量很大，可能还容易Overfitting

所以有没有更好的方法，来考虑整个Input Sequence的信息呢，这就要用到Self-Attention（自注意力）这个机制。

Self-Attention

简介

Self-Attention的运作方式就是，Self-Attention会接收一整个Sequence的信息，然后你Input几个Vector，它就输出几个Vector，这边输入4个Vector，它就Output 4个Vector
，这4个Vector，他们都是考虑一整个Sequence以后才得到的。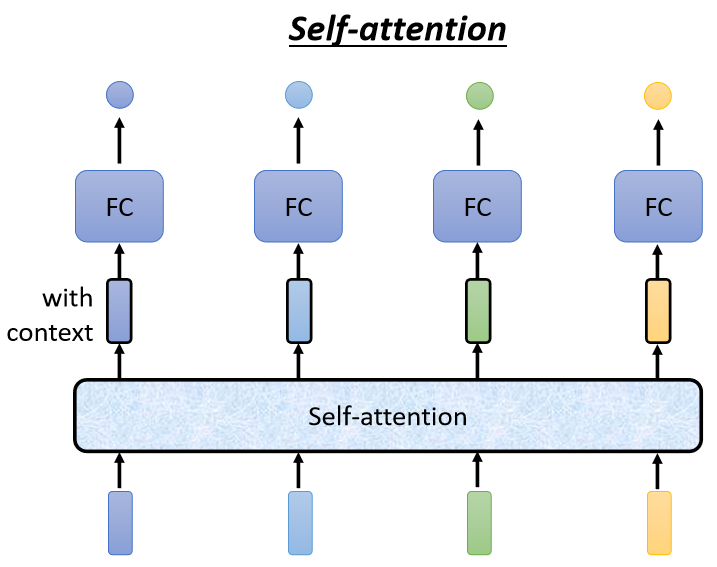

如此一来，Fully-Connected Network就不是只考虑一个非常小的范围，而是考虑整个Sequence的信息，再来决定现在应该要输出什么样的结果，这个就是Self-Attention。

Self-Attention可以叠加使用。

Fully-Connected Network，跟Self-Attention交替使用，Self-Attention处理整个Sequence的信息，Fully-Connected Network专注于处理某一个位置的信息，
再用Self-Attention，再把整个Sequence信息再处理一次，然后交替使用Self-Attention跟Fully-Connected。

Self-Attention过程

Self-Attention的Input，它就是一串的Vector，那这串Vector可能是你整个Network的Input，它也可能是某个Hidden Layer的Output，所以我们这边不用$x$来表示它，我们用$a$来表示它，代表它有可能是前面已经做过一些处理，它是某个Hidden Layer的Output，那Input一排a这个向量以后，Self-Attention要Output另外一排$b$这个向量。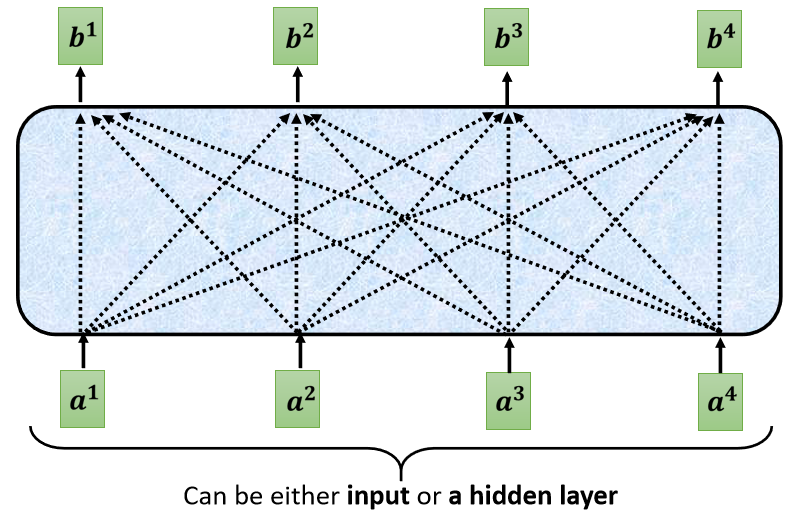

每一个b都是考虑了所有的a以后才生成出来的，所以这边刻意画了非常非常多的箭头，告诉你$b^1$考虑了$a^1$到$a^4$产生的，$b^2$考虑了$a^1$到$a^4$产生的，b3b4也都是考虑整个input的sequence才产生的。
以$b^1$为例，阐述b产生过程。
这里有一个特别的机制，这个机制是根据$a^1$这个向量找出整个很长的sequence里面，到底哪些部分是重要的，哪些部分跟判断$a^1$是哪一个label有关系的，哪些部分是我们要决定$a^1$的class，决定$a^1$的regression数值的时候，所需要用到的信息。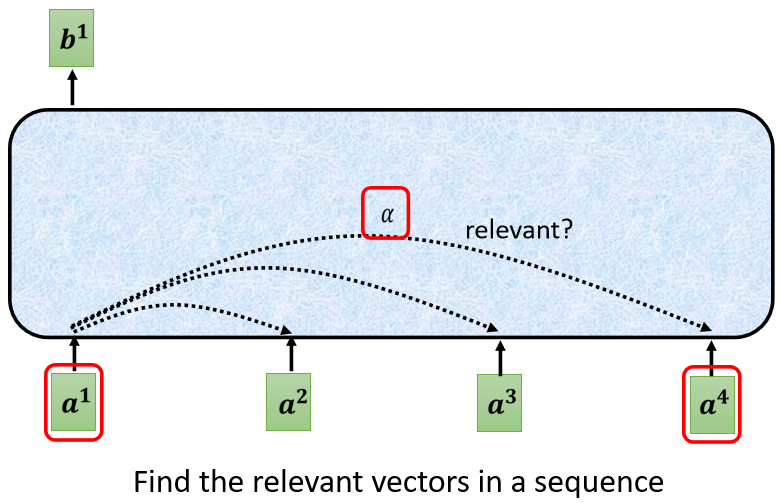

每一个向量跟$a^1$的关联的程度，用一个数值叫α来表示。

self-attention的module，怎么自动决定两个向量之间的关联性呢，你给它两个向量$a^1$跟$a^4$，它怎么决定$a^1$跟$a^4$有多相关，然后给它一个数值α，这边需要一个计算attention的模组。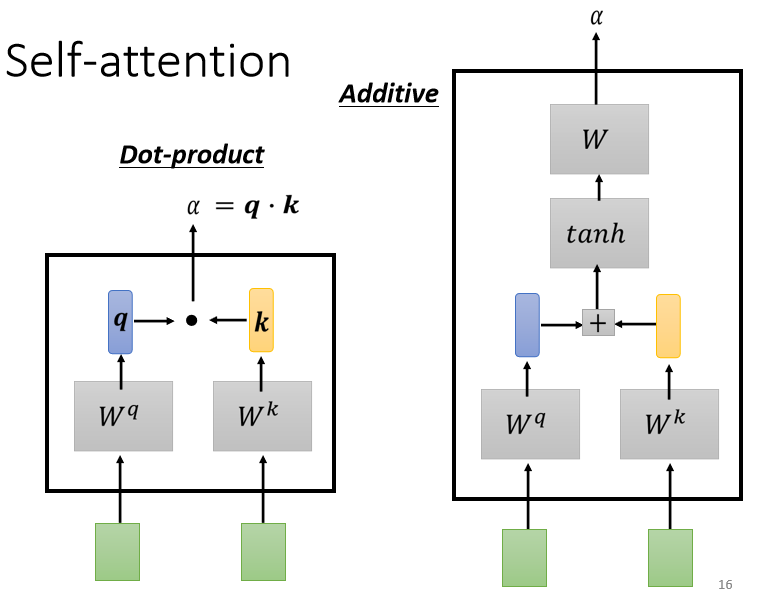

计算attention的模组拿两个向量作为输入，然后直接输出α那个数值，计算这个α的数值有各种不同的做法，我们提一种方法，这是今日最常用的方法，也是用在Transformer里面的方法:

• 用dot product（数量积），输入的这两个向量分别乘上两个不同的矩阵，左边这个向量乘上$W^q$矩阵得到矩阵q，右边这个向量乘上$W^k$矩阵得到矩阵k。
• q与k做dot product（把他们做element-wise的相乘再全部加起来）以后就得到一个scalar，这个scalar就是α。

我们需要把$a^1$去跟$a^2a^3a^4$，分别都去计算他们之间的关联性，也就是计算他们之间的α，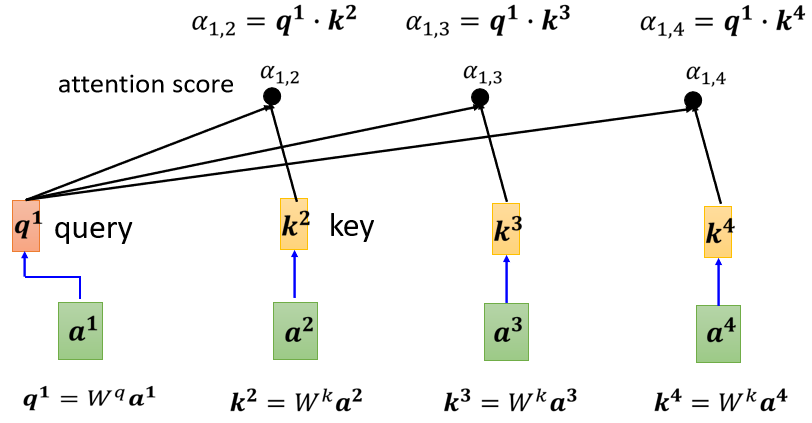

• 你把$a^1$乘上$W^q$得到$q^1$，q我们叫做Query，它就像是你搜寻相关文章的关键字，所以这边叫做Query，然后$a^2a^3a^4$都要乘上$W^k$，得到$k$这个Vector，这个Vector叫做Key。

• 把Query q1，跟这个Key k2，算dot product就得到$\alpha_{1,2}$（往往除以维度的平方根，使得梯度更加稳定）。

• $\alpha_{1,2}$代表Query是1提供的，Key是2提供的时候，这个1跟2他们之间的关联性，α的这个关联性也叫做Attention的Score，以此类推$\alpha_{1,3}$，$\alpha_{1,4}$ 。

实际中，$a^1$也会跟自己算关联性。

计算出，a1跟每一个向量的关联性以后，接下来这边会接入一个Soft-Max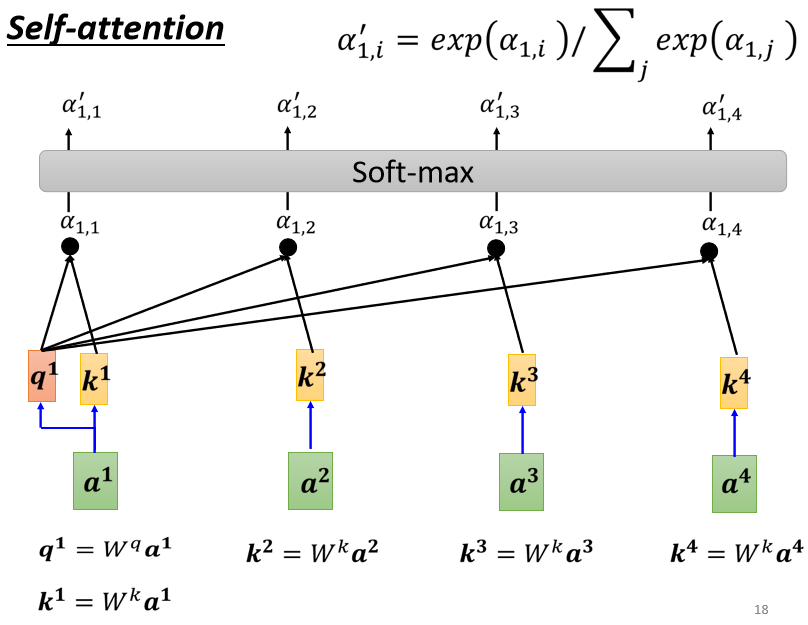

这个Soft-Max跟分类的时候的那个Soft-Max是一模一样的，所以Soft-Max的输出就是一排α，这一排α通过Soft-Max就得到$\alpha^\prime$。

这边不一定要用Soft-Max，用别的替代也没问题，比如说有人尝试过做ReLU，结果发现还比Soft-Max好一点，其实不一定要用Soft-Max，这边你要用什么Activation Function都行，Soft-Max是最常见的，可以自己尝试，看能不能试出比Soft-Max更好的结果。

得到$\alpha^\prime$以后，我们要根据这个$\alpha^\prime$去抽取出这个Sequence里面重要的信息，根据这个α我们已经知道哪些向量跟$a^1$是最有关系的，怎么抽取重要的信息呢？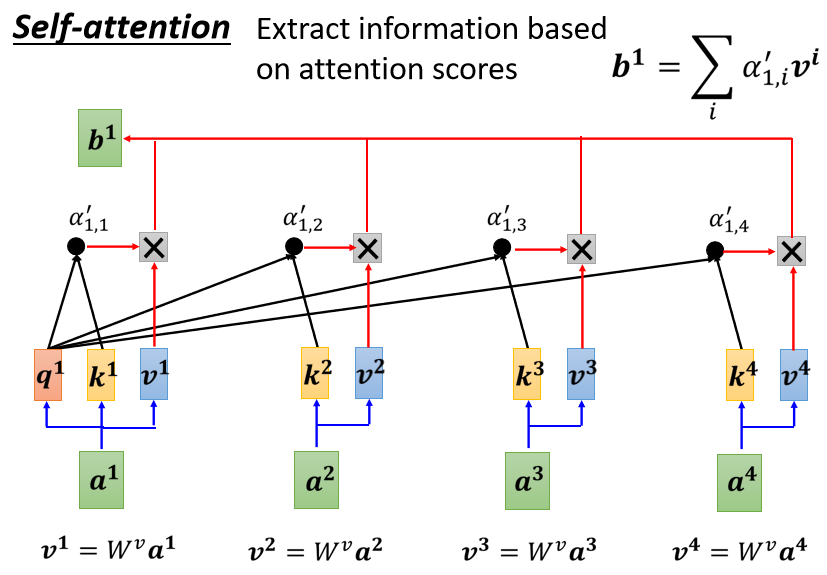

• 首先把$a^1$到$a^4$这边每一个向量乘上$W^v$得到新的向量，这边分别用$v^1v^2v^3v^4$来表示。
• 接下来把这边的$v^1$到$v^4$，每一个向量都去乘上Attention的分数（$\alpha^\prime$），
• 然后再把它加起来，得到b1

如果某一个向量它得到的分数越高，比如说$a^1$跟$a^2$的关联性很强，$\alpha^\prime$得到的值很大，那我们今天在做Weighted Sum以后得到的的值，就可能会比较接近$v^2$。

所以谁的Attention的分数最大，谁的$v$就会Dominant你抽出来的结果，这边就讲了怎么从一整个Sequence得到$b^1$。

从这一排vector得到$b^2$，跟从这一排vector得到$b^1$的操作是一模一样的。要强调一点是$b^1$到$b^4$，它们并不需要依序产生，它们是一次同时被计算出来的。

从矩阵的角度Self-Attention过程

我们已知每一个a都产生q k v，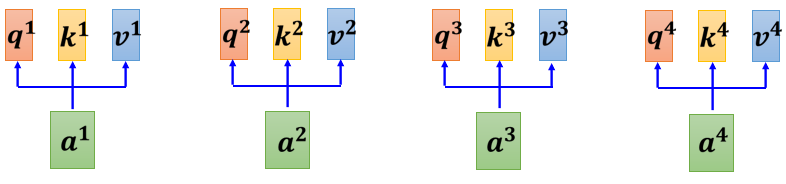

用矩阵运算表示这个操作，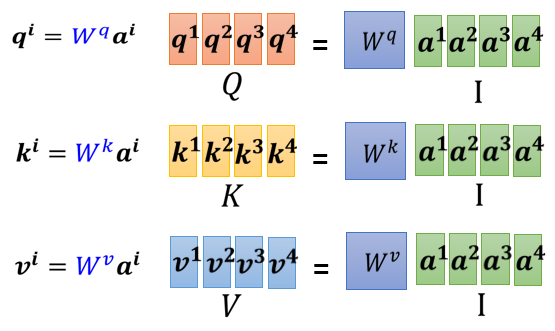

每一个a都要乘上$W^q$，得到$q^i$，这些不同的a你可以把它合起来，当作一个矩阵来看待，这个矩阵我们用I来表示，这个矩阵的四个column就是$a^1$到$a^4$，I乘上$W^q$就得到另外一个矩阵$Q$，$Q$就是把$q^1$到$q^4$这四个vector拼起来，就是$Q$的四个column，$W^q$其实是network的参数，它是会被learn出来的。

接下来产生k跟v的操作跟q是一模一样的，vector sequence乘上三个不同的矩阵，你就得到了q，k，v。

下一步是，每一个q都会去跟每一个k，去计算attention的分数，得到attention分数这一件事情，如果从矩阵操作的角度来看，它在做什么样的事情呢？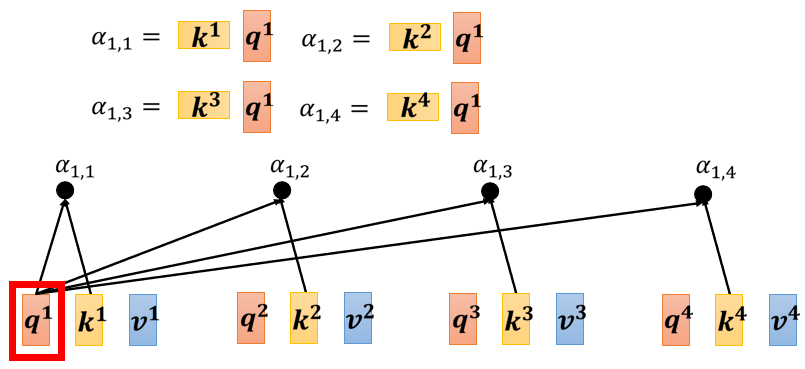

$q^1$跟$k^1$做inner product得到$α_{1,1}$，实际上是$k^1$的transpose与$q^1$向量乘法，以此类推四次，那四次的操作，其实可以把它拼起来，看作是矩阵跟向量相乘。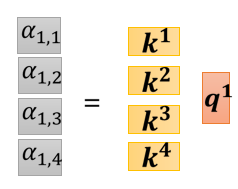

那从$q^1$以此类推四次，那四次的操作，其实可以把它拼起来，看作是矩阵跟矩阵相乘。

我们会把attention的分数，做一下normalization，比如softmax，你会对这边的每一个column，每一个column做softmax，让每一个column里面的值相加是1，我们用$A^\prime$来表示通过softmax以后的结果。

把$v^1$到$v^4$当成是V这个矩阵的四个column，然后接下来你把v乘上$A^\prime$的第一个column以后，你得到的结果就是$b^1$（线性代数），以此类推，最后如图得到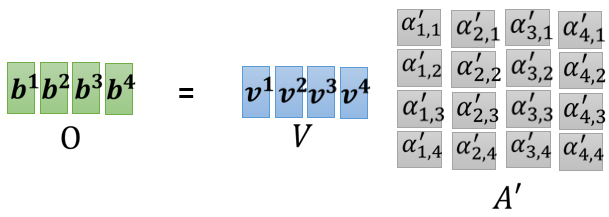

所以我们等于就是把$A^\prime$这个矩阵，乘上V这个矩阵，得到O这个矩阵，O这个矩阵里面的每一个column，就是Self-attention的输出，也就是$b^1$到$b^4$。

总结如下图：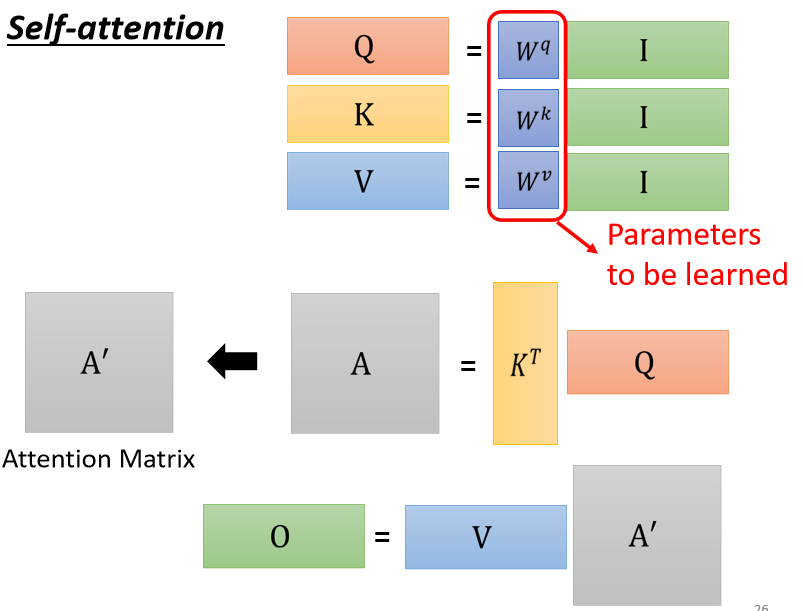

Multi-head Self-attention

Self-attention 进阶的版本 Multi-head Self-attention今天的使用非常广泛。

我们在做这个Self-attention的时候，我们就是用q去找相关的k，但是相关这件事情有很多种不同的形式，有很多种不同的定义，所以我们不能只有一个q，我们应该要有多个q，不同的q负责不同种类的相关性。

需要用多少的head，这个又是另外一个hyperparameter。

以两个head为例: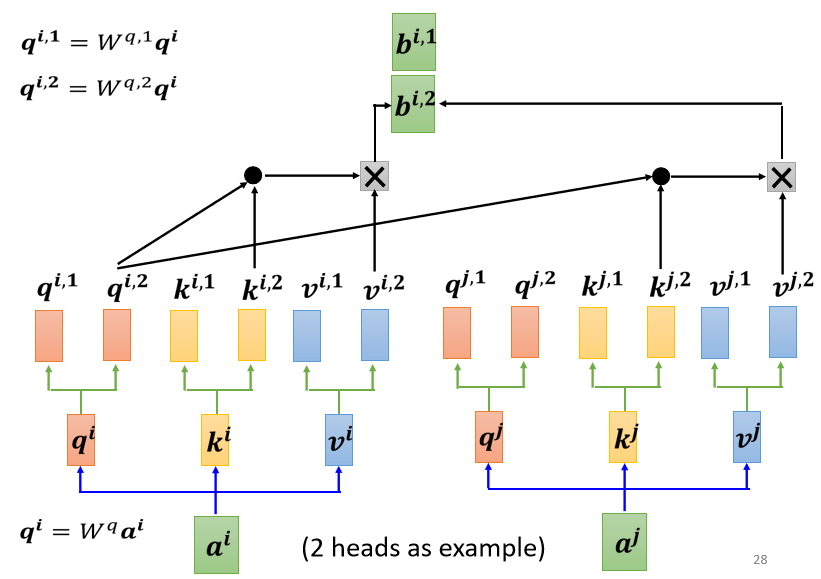

总之，各忙各的。
i是指$a^i$的上角标，$b^{i,1}$是$a^i$在第一个head下的输出，$b^{i,2}$是$a^i$在第二个head下的输出。
接下来你可能会把$b^{i,1}$与$b^{i,2}$接起来，然后再通过一个 transform也就是再乘上一个矩阵，然后得到 bi，再送到下一层去，这个就是 Multi-head attention，一个 Self-attention 的变形。

Positional Encoding

思考到现在，你会发现Self-attention的layer少了一个也许很重要的信息，这个信息是位置的信息

对一个Self-attention layer而言，每一个input，它是出现在sequence的最前面，还是最后面，它是完全没有这个信息的。

所以对Self-attention而言，位置1跟位置2跟位置3跟位置4，完全没有任何差别，这四个位置的操作其实是一模一样，对它来说q1到跟q4的距离，并没有特别远，2跟3的距离也没有特别近。

但是这样设计可能会有一些问题，因为有时候位置的信息也许很重要，举例来说，我们在做这个POS tagging，就是词性标记的时候，比如你知道说动词比较不容易出现在句首，所以如果我们知道某一个词汇它是放在句首的，那它是动词的可能性可能就比较低，这样子的位置的信息往往也是有用的。

我们采用positional encoding（位置编码）的方法去添加位置信息。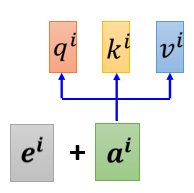

我们为每一个位置设定一个vector，叫做positional vector，这边用$e^i$来表示，上标i代表是位置，每一个不同的位置，就有不同的vector，比如$e^1$是一个vector，$e^2$是一个vector，$e^112$是一个vector，不同的位置都有一个它专属的e，然后把这个e加到$a^i$上面作为新的$a^i$参与后面的运算过程，就结束了。

positional encoding的具体方法仍然是一个尚待研究的问题，你可以创造自己新的方法，或甚至positional encoding，是可以根据数据学出来的。
在 Transformer 中采用了手工设计的公式，计算公式如下：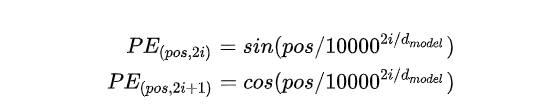

pos表示token在sequence中的位置，i或者准确以上是2i和2i+1便是了positionnal encoding的维度，i的取值范围是：[0,……，$d_{model/2}$)。底数是10000，为什么要使用10000呢？这个就类似于玄学了，原论文中完全没有提，这里不得不说说论文的readability的问题，即便是很多高引的文章，最基本的内容都讨论不清楚，所以才出现像上面提问里的讨论，说实话这些论文还远远没有做到easy to follow。
关于positional encoding和三角函数有什么关系？可以参照这位的理解

Applications for Image

其实一张图片，我们也可以换一个观点，把它看作是一个vector的set，一个分辨率5乘以10的图片可以看作是一个tensor，这个tensor的大小是5乘以10乘以3，3代表RGB这3个channel。（笔者研究图像处理，所以对于attention在并行化上甩开RNN等自然语言处理方向问题不再赘述）

你可以把每一个位置的pixel，看作是一个三维的向量，所以每一个pixel，其实就是一个三维的向量，那整张图片，其实就是5乘以10个向量的set。

所以我们其实可以换一个角度，图像这个东西，其实也是一个vector set，它既然也是一个vector set的话，你完全可以用Self-attention来处理一张图片。

我们可以来比较一下，Self-attention跟CNN之间，有什么样的差异或者是关联性。

如果我们今天用Self-attention来处理一张图片，假设这个是你要考虑的pixel，那它产生query，其他pixel产生key，

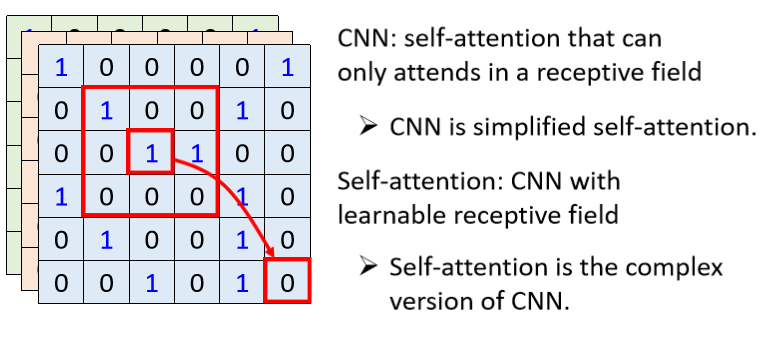
我们在做inner product的时候，你考虑的不是一个小的receptive field的信息，而是整张图像的信息

但是在做CNN的时候，会画出一个receptive field，每一个filter，每一个neural，只考虑receptive field范围里面的信息。

所以比较CNN跟Self-attention的话，CNN可以看作是一种简化版的Self-attention，因为在做CNN的时候，我们只考虑receptive field里面的信息，而在做Self-attention的时候，我们是考虑整张图片的信息，或者是你可以反过来说，Self-attention是一个复杂化的CNN。

在CNN里面，我们要划定receptive field，每一个neural，只考虑receptive field里面的信息，而receptive field的范围跟大小，是人决定的，而对Self-attention而言，我们用attention，去找出相关的pixel，就好像是receptive field是自动被学出的，network自己决定receptive field的形状长什么样子，network自己决定说，以这个pixel为中心，哪些pixel是我们真正需要考虑的，哪些pixel是相关的。
所以receptive field的范围，不再是人工划定，而是让机器自己学出来。

在这篇paper里面，会用数学的方式严谨的告诉你说，其实CNN就是Self-attention的特例，Self-attention只要设定合适的参数，它可以做到跟CNN一模一样的事情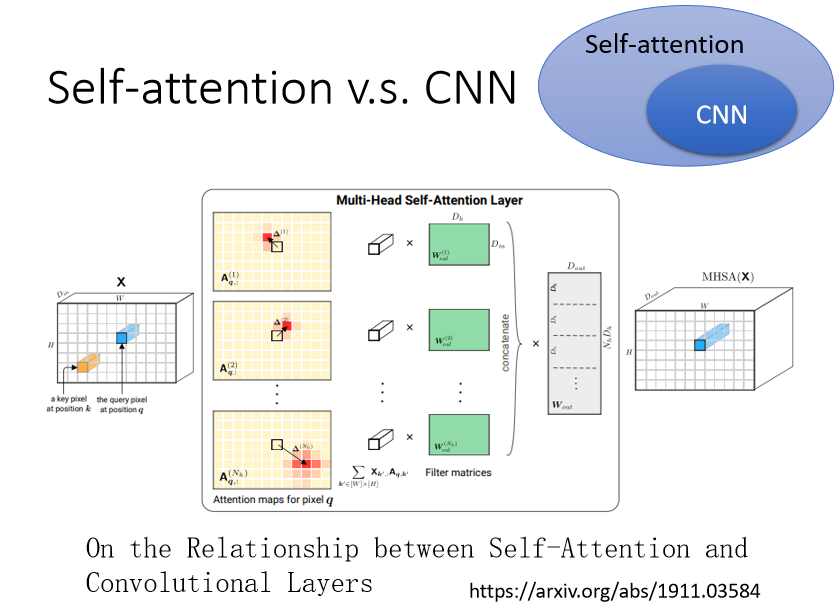

所以self attention，是更flexible的CNN，而CNN是有受限制的Self-attention，Self-attention只要通过某些设计和限制，它就会变成CNN。

所以Self-attention它弹性比较大，所以需要比较多的训练数据，训练数据少的时候，就会overfitting
而CNN它弹性比较小，在训练数据少的时候，结果比较好，但训练数据多的时候，它没有办法从更大量的训练数据得到好处，如下图实验结果：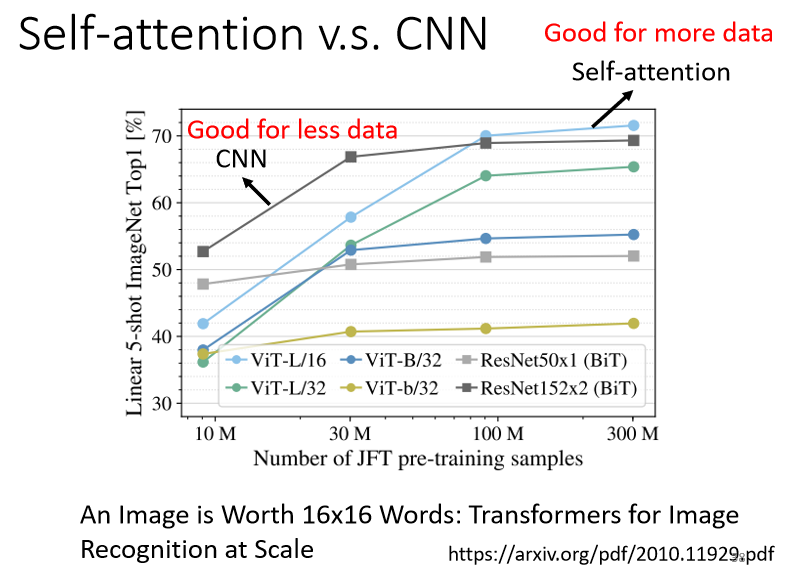

问题

Self-attention有非常非常多的变形，你可以看一篇paper叫做Long Range Arena，里面比较了各种不同的Self-attention的变形: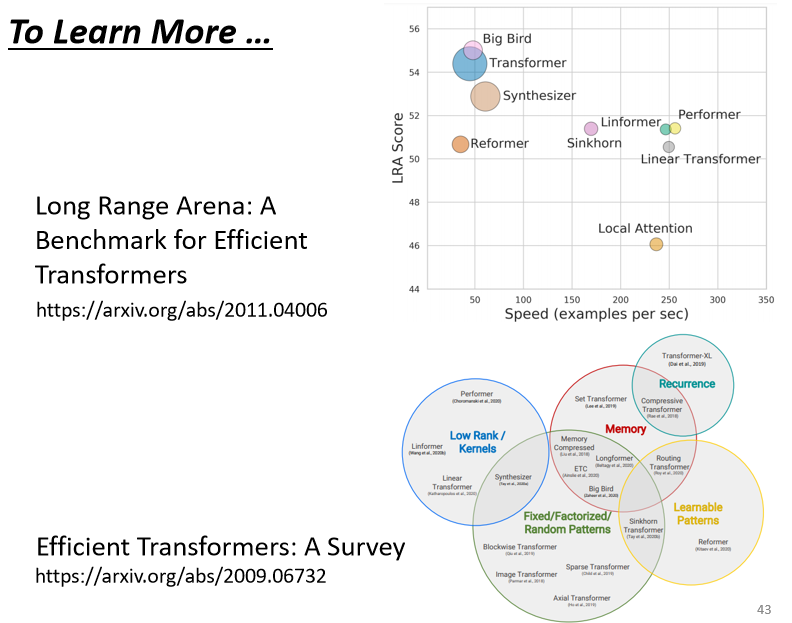

Self-attention它最大的问题就是，它的运算量非常地大，所以怎么样减少Self-attention的运算量，是一个未来的重点，可以看到这边有各种Self-attention的变形。

可以看到，横轴代表它运算的速度，纵轴代表是performance，所以有很多各式各样新的xxformer，它们的速度会比原来的Transformer快，但是快的速度带来的就是performance变差，到底什么样的Self-attention，才能够又快又好，这仍然是一个尚待研究的问题。